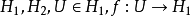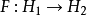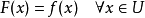利普希茨連續

在數學中，特別是實分析，利普希茨連續（Lipschitz continuity）以德國數學家魯道夫·利普希茨命名，是一個比通常連續更強的光滑性條件。直覺上，利普希茨連續函式限制了函式改變的速度，符合利普希茨條件的函式的斜率，必小於一個稱為利普希茨常數的實數（該常數依函式而定）。

在微分方程中，利普希茨連續是皮卡-林德洛夫定理中確保了初值問題存在唯一解的核心條件。一種特殊的利普希茨連續，稱為壓縮套用於巴拿赫不動點定理。

利普希茨連續可以定義在度量空間上以及賦范向量空間上；利普希茨連續的一種推廣稱為赫爾德連續。

基本介紹

• 中文名：利普希茨連續
• 外文名：Lipschitz continuity
• 提出人：魯道夫·利普希茨
• 套用範圍：實分析、微積分

定義

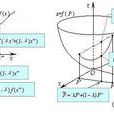
對於在實數集的子集的函式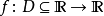 ，若存在常數K，使得 ，則稱 f 符合利普希茨條件，對於f 最小的常數K 稱為 f 的利普希茨常數。

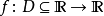
若K < 1，f 稱為收縮映射。

利普希茨條件也可對任意度量空間的函式定義：

給定兩個度量空間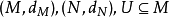 。若對於函式 ，存在常數K 使得

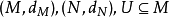
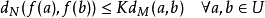
則說它符合利普希茨條件。

若存在K ≥ 1使得

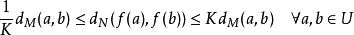
則稱 f 為雙李普希茨(bi-Lipschitz)的。

定理

(此定理又稱柯西-利普希茨定理）若已知y(t)有界，f 符合利普希茨條件，則微分方程初值問題 剛好有一個解。

在套用上，t通常屬於一有界閉區間（如 ）。於是y(t)必有界，故y有唯一解。

例子

符合利普希茨條件，K=14。

不符合利普希茨條件，當 。

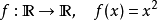
定義在所有實數值的 符合利普希茨條件，K=1。

符合利普希茨條件，K=1。由此可見符合利普希茨條件的函式未必可微。

不符合利普希茨條件， 。不過，它符合赫爾德條件。

若且唯若處處可微函式f的一次導函式有界，f符利普希茨條件。這是中值定理的結果。所有C¹函式都是局部利普希茨的，因為局部緊緻空間的連續函式必定有界。

性質

符合利普希茨條件的函式一致連續，也連續。

bi-Lipschitz函式是單射的。

Rademacher定理：若 且A為開集， 符利普希茨條件，則f幾乎處處可微。

Kirszbraun定理：給定兩個希爾伯特空間 符合利普希茨條件，則存在符合利普希茨條件的，使得F的利普希茨常數和f的相同，且 。