巴拿赫不動點定理

定理

設(X,d)為非空的完備度量空間。設T:X→X為X上的一個壓縮映射，也就是說，存在一個非負的實數q<1，使得對於所有X內的x和y，都有：

那么映射T在X內有且只有一個不動點x（這就是說，Tx=x）。更進一步，這個不動點可以用以下的方法來求出：從X內的任意一個元素x₀開始，並定義一個疊代序列x_n=Tx_n_-1，對於n= 1，2，3，……。這個序列收斂，且極限為x。以下的不等式描述了收斂的速率：

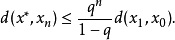
等價地：

且

滿足以上不等式的最小的q有時稱為利普希茨常數。

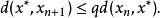
注意對於所有不同的x和y都有d(Tx,Ty) < d(x,y)的要求，一般來說是不足以保證不動點的存在的，例如映射T: [1,∞) → [1,∞)，T(x) =x+ 1/x，就沒有不動點。但是，如果空間X是緊的，則這個較弱的假設也能保證不動點的存在。

當實際套用這個定理時，最艱難的部分通常是恰當地定義X，使得T實際上把元素從X映射到X，也就是說，Tx總是X的一個元素。

巴拿赫不動點定理有許多逆定理，以下的一個是Czesław Bessaga在1959年發現的：

設

為一個抽象集合的映射，使得每一個疊代f都有一個唯一的不動點。設q為一個實數，0 < q < 1。那么存在X上的一個完備度量，使得f是壓縮映射，且q是壓縮常數。

一個有趣的事實是，若把某國的地圖縮小後印在該國領土內部，那么在地圖上有且僅有這樣一個點，它在地圖中的位置也恰巧表示它所落在的土地位置。證明如下：

為了方便起見，這裡把地球近似看作是正球體。
首先，按照經緯度可以給地球表面上每一個點標出坐標 (x, y)，其中前元是經度、後元是緯度。又定義地面上任意兩點間的距離 d(A, B) 是 A 到 B 間大圓弧的弧長。
其次，把這國家的地圖上的點按照其所代表點的實際經緯度標出坐標 (u, v)。
那么對於地圖上任意一點 P 而言，它既在地圖上表示地點 (up, vp)，又實際在地面上占有點 (xp, yp)。顯然，這構成了從集合 S={P|P 是地面上的點且 P 屬於該國領土} 到其本身的映射，現記作 M(P)=M((up, vp))=(xp, yp)。
又因為地圖是縮小的，即對於任意兩個地點 A∈S、B∈S 而言，d(A, B)>d(M(A), M(B))，也即 M(P) 是一個壓縮映射。
事實上，取實數 k>1 作為地圖比例尺的分母、即 1:k，那么由比例尺的定義知 d(A, B)=kd(M(A), M(B))，兩邊同除以 k 得 d(A, B)*(1/k)=d(M(A), M(B))。換言之，存在實數 q=1/k<1 滿足對於 S 內所有的 A 和 B，d(M(A), M(B))≤qd(A, B)，這裡等號總是成立。
現在將 S 視為以 d 為度量的空間，那么它顯然是一個完備度量空間。
根據巴拿赫不動點定理，M 在 S 內有且僅有一個不動點，即該點恰好被印在它所表示的土地位置上。Q.E.D.