一般指半徑為R的圓中,n°的圓心角所對弧長為nπR/180°,廣義上指光滑曲線的弧長。
基本介紹
- 中文名:弧長
- 外文名:arc length
- 所屬學科:數理科學
- 相關概念:連續曲線、光滑曲線、連續可導等
基本概念
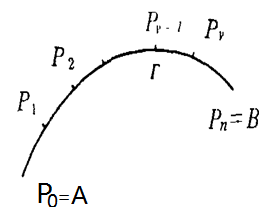 圖1曲線的弧長
圖1曲線的弧長設




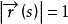
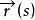

弧長的計算
 圖2
圖2
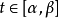

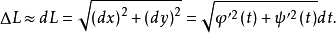
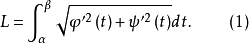
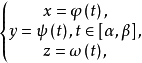

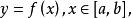
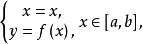

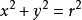
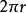
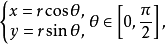

扇形的弧長與計算公式
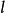
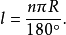

一般指半徑為R的圓中,n°的圓心角所對弧長為nπR/180°,廣義上指光滑曲線的弧長。
 圖1曲線的弧長
圖1曲線的弧長



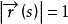
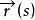

 圖2
圖2
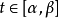

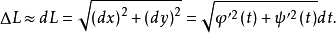
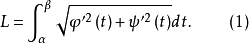
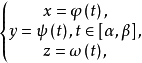

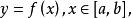
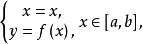

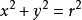
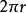
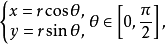

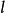
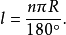
一般指半徑為R的圓中,n°的圓心角所對弧長為nπR/180°,廣義上指光滑曲線的弧長。...... 一般指半徑為R的圓中,n°的圓心角所對弧長為nπR/180°,廣義上...
弧長計算公式是一個數學公式,為L=n× π× r/180,L=α× r。其中n是圓心角度數,r是半徑,L是圓心角弧長。...
扇形弧長是扇形的兩條半徑之間的圓弧長度,一條圓弧和經過這條圓弧兩端的兩條半徑所圍成的圖形叫扇形,弧長=半徑×圓心角弧度數。...
弧長公式是平面幾何的基本公式之一。弧長公式敘述了弧長,即在圓上過兩點的一段弧的長度,與半徑和圓心角的關係。公式為:l=πrα/180...
弧,也稱圓弧,拼音hú,意為圓周上任意的一段。弧的大小的兩種表示:弧長與圓心角(弧度數)。弧長計算公式:L = n π r/180...
弧長函式(arc length function),是指量度弧長的函式。設Γ為定義在[a,b]上的可求長曲線,對t∈[a,b],Γ的參數表示φ對[a,t]的限制所表示的曲線的長度記...
弧微分是用一條線段的長度來近似代表一段弧的長度。設函式f(x)在區間(a,b)內具有連續導數,在曲線Y=f(x)上取定點Mo(xo,f(xo))作為計算曲線弧長的基點,M...
弧長第一變分公式(first variation formula ofarc length)曲線族弧長泛函的一階導數公式.設Y(t) (a<t
臀部弧長(gluteal arc):在經臀溝最下緣的垂直線上,從最小腰圍部位至臀溝下緣的弧長。...
弧長控制,主要由電感、電容濾波電路,二極體、穩壓管整流限幅電路和光耦隔離電路組成。...
弧,一般可解釋為:(1)平面角的一種量度單位,其大小等於角所對的弧長被半徑除的商,1弧度等於180=57.3【弧度】;(2)一種持續的耀眼亮光,有時具有輝光弧線的...
在數學和物理中,弧度是角的度量單位。它是由國際單位制導出的單位,單位縮寫是rad。定義:弧長等於半徑的弧,其所對的圓心角為1弧度。(即兩條射線從圓心向圓周射出...
用弧長與半徑之比度量對應圓心角角度的方式,叫做弧度制,用符號rad表示,讀作弧度。等於半徑長的圓弧所對的圓心角叫做1弧度的角。由於圓弧長短與圓半徑之比,不因為...
,l是弧長,|α|是弧l所對的圓心角的弧度數的絕對值,R是扇形半徑。 弧長公式 面積公式 R是扇形半徑,n是弧所對圓心角度數,π是圓周率,L是扇形對應的弧長。 ...
在L的取法無關,則稱極限值為f(x,y)在L上對弧長的曲線積分,記為: ;其中f(x,y)叫做被積函式,L叫做積分曲線,對弧長的曲線積分也叫第一類曲線積分。(...
扇形還與三角形有相似之處,上述簡化的面積公式亦可看成:1/2×弧長×半徑,與三角形面積:1/2×底×高相似。扇形面積 公式: S扇=(lR)/2 (l為扇形弧長) =(...
圓周角定理指的是一條弧所對圓周角等於它所對圓心角的一半。這一定理叫做圓周角定理。該定理反映的是圓周角與圓心角的關係。中文名 圓周角定理 外文名 The ...
在右圖中,θ是扇形的角弧度,r是圓的半徑,L是小扇形的弧長。[1] 圓弧為180°的扇形稱為半圓。其他圓弧角的扇形有時給予其特別的名字,其中包括象限角(90°)、...
曲線的曲率(curvature)就是針對曲線上某個點的切線方向角對弧長的轉動率,通過微分來定義,表明曲線偏離直線的程度。數學上表明曲線在某一點的彎曲程度的數值。曲率越...
在微分幾何中,曲率的倒數就是曲率半徑,即R=1/K。平面曲線的曲率就是針對曲線上某個點的切線方向角對弧長的轉動率,通過微分來定義,表明曲線偏離直線的程度。對於...
