設含有n個未知數與n個方程的非線性方程組為F(x)=0,然後把方程組改為便於疊代的等價形式x=ψ(x),由此就可以構造出不動點疊代法的疊代公式為xk+1=ψ(xk),如果得到的序列{xk}滿足lim(k→∞)xk=x*,則x*就是ψ的不動點,這樣就可以求出非線性方程組的解。
基本介紹
- 中文名:不動點法
- 外文名:fixed point method
- 所屬領域:數理科學
- 套用:研究方程解的存在、唯一性和計算
- 相關概念:不動點定理、運算元方程等
方法簡介







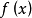


舉例說明


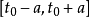



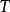

注意點
不動點定理
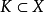





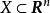





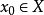
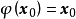

設含有n個未知數與n個方程的非線性方程組為F(x)=0,然後把方程組改為便於疊代的等價形式x=ψ(x),由此就可以構造出不動點疊代法的疊代公式為xk+1=ψ(xk),如果得到的序列{xk}滿足lim(k→∞)xk=x*,則x*就是ψ的不動點,這樣就可以求出非線性方程組的解。







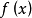




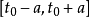



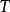

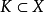





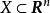





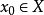
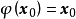
設含有n個未知數與n個方程的非線性方程組為F(x)=0,然後把方程組改為便於疊代的等價形式x=ψ(x),由此就可以構造出不動點疊代法的疊代公式為xk+1=ψ(xk),...
本書從一道28屆IMO試題談起,首先介紹了在數學競賽中的不動點問題,列舉了很多中外數學競賽中有關不動點問題的例題,其次本書還介紹了高等數學中的不動點問題,詳細...
本書主要介紹了布勞維不動點定理及其推廣角谷靜夫不動點定理的證明及套用。全書共分為6章:第1章,布勞維不動點定理;第2章,某些非線性微分方程的周期解的存在性;...
書籍信息書名不動點與零點的疊代方法及其套用 書號978-7-118-10939-9 作者周海雲 出版時間2016年6月 譯者 版次1版1次 開本16 裝幀精裝 出版基金國防科技圖書...
的性質,就是由成倍遞增的一組數所組成的數列.求和公式,可用錯位相減法推出 [...不動點法(常用於分式的通項遞推關係)數列公式特殊常見的 ①數列1,2,3,4,5...
主要從事微分方程問題研究,近年發表的主要論文有:1、《關於非線性奇異性(n+1)階邊質問題的單調性方法》哈師大報2、《關於非線性奇異性(n+1)階邊質問題的不動...
不動點法(常用於分式的通項遞推關係)不動點法求數列通項對於某些特定形式的數列遞推式可用不動點法來求遞推數列特殊數列 編輯 ...
四、圖解法五、不動點方法的推廣六、Stolz公式的套用§1.6序列的上、下極限一、利用ε-N語言描述上、下極限二、利用子序列的極限描述上、下極限...
壓縮映射法是不動點法中一種常用的方法。它的根據是壓縮映射原理:設X是一個完備的距離空間,f是從X到X的一個壓縮映射,那么f在X中必有且僅有一個不動點,...
1995年提出接觸問題非線性互補算法,1997年提出不協調元強分片檢驗條件,2000年提出接觸問題的非光滑算法和不動點法,2000年-至今,建立了解除閉鎖的高精度的三角形和...
Radu用 不動點方法解決 Hyers-Ulam 穩定性問題,之後,直 接方法和不動點方法成為研究函式方程穩定性的重 要方法.函式方程F具有超穩定性,是指如果對任意的 函式f...
在非線性問題的研究中,除不動點方法外,拓撲度方法和變分法都是十分有效的工具。[1] 偽非定常法疊代解法 編輯 疊代解法是用逐次逼近解高階線性代數方程組的一...
4.1.2 待定係數法4.1.3 不動點法4.1.4 階差法4.1.5 直接代換法4.1.6 變形轉化法4.1 _7數學歸納法好題新題精選(七)4.2 了解放縮技巧...
