里斯引理

里斯引理（Riesz lemma）揭示閉子空間與單位球面上某點的距離性質的重要引理。

基本介紹

• 中文名：里斯引理
• 外文名：Riesz lemma
• 適用範圍：數理科學

簡介

里斯引理揭示閉子空間與單位球面上某點的距離性質的重要引理。

設Y是賦范線性空間X的閉線性真子空間，則對任何ε>(0,1)，存在x∈X，||x||=1，使得d(x,Y)≥ε，其中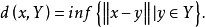

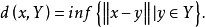
套用

里斯引理是里斯(Riesz,F.)於1918年得到的，它在泛函分析中有著廣泛的套用。例如，由里斯引理可得，賦范線性空間X的每一個有界閉集是緊的若且唯若X是有限維空間。

1975年，考特曼(Kottman,C.A.)把里斯引理向前大大推進了一步：設X是無窮維賦范線性空間，則存在點列{X_n}⊂X，||x_n||=1，使得當m≠n時，有||x_m-x_n||>1。

考特曼的這一定理在巴拿赫空間局部理論的研究中有重要作用，特別是在填球問題(parking problem)中扮演重要角色。

賦范線性空間

(normed linear space)

賦范線性空間是線上性空間中引進一種與代數運算相聯繫的度量，即由向量範數誘導出的度量。賦范線性空間稱為Banach空間，是指由範數導出的度量是完備的。