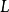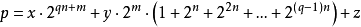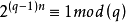泵引理

泵引理是形式語言與自動機理論中判定一個語言不是正則語言的重要工具，下面介紹的是其通用的形式，除此之外還有其推廣的強泵引理等。

基本介紹

• 中文名：泵引理
• 外文名：pumping lemma
• 類型：工具
• 範圍：形式語言與自動機理論
• 有關學科：數學等

簡介

在可計算性理論中的形式語言理論中，泵引理聲稱給定類的任何語言可以被“抽吸”並仍屬於這個類。一個語言可以被抽吸，如果在這個語言中任何足夠長的字元串可以分解成片段，其中某些可以任意重複來生成語言中更長的字元串。這些引理的證明典型的需要計數論證比如鴿籠原理。

兩個最重要例子是正則語言的泵引理和上下文無關語言的泵引理。鄂登引理是另一種更強的上下文無關語言的泵引理。

這些引理可以用來確定特定語言不在給定語言類中。但是它們不能被用來確定一個語言在給定類中，因為滿足引理是類成員關係的必要條件，但不是充分條件。

泵引理是1961年由Y. Bar-Hillel、M. Perles和E. Shamir首次發表的。

引理描述

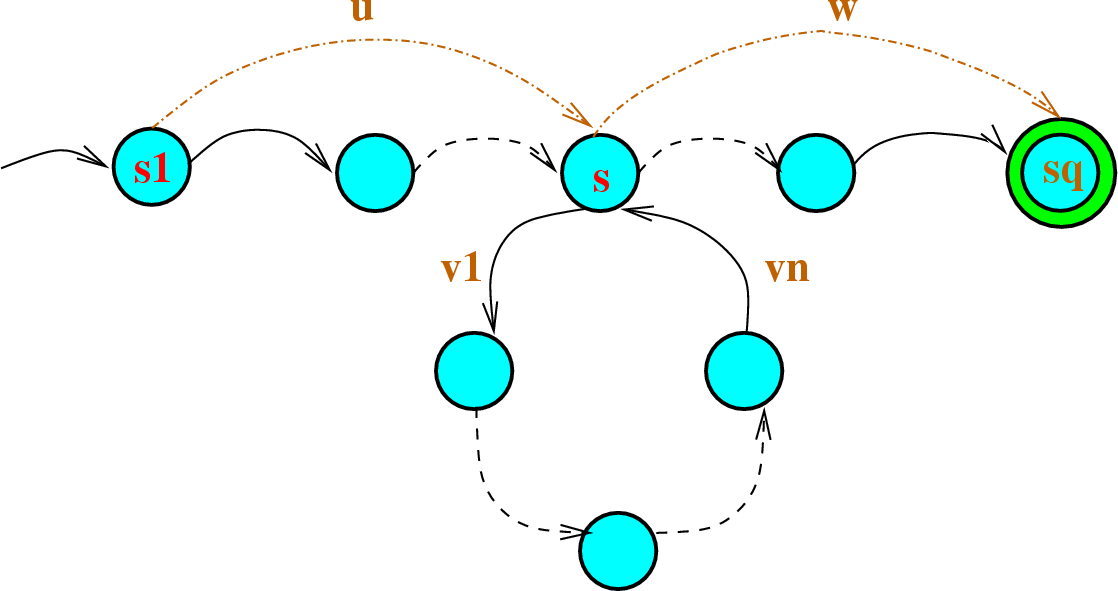
若 L 是正則語言，則存在一常數 n > 0 ，對於語言 L 中每個滿足|w| ≥ n的字元串w，存在一組x,y,z使得，w=xyz且：

1.|xy| ≤ n ；

2.|y| ≥ 1；

3.對所有的 k ≥ 0 ，字串 屬於 L 。

證：若L為正則語言，那么存在一個DFA識別它。設其狀態數為n，那么對於任意字元串w∈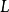它被DFA識別時的狀態轉換為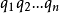：（qn為接受狀態）。因為w≥ n，所以由鴿籠原理存在狀態重複，記狀態所識別的字元串為y，那么易知（即是將重複狀態重複k次）仍可被此DFA識別，故∈。

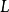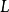
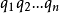
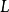
引理套用

例1：字元串集合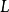={ | m,n∈N ∧ n>m }不是正則的。

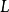
證明：顯然∈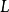，所以由泵引理知當p足夠大時字元串中存在子串可重複。若該子串中只有0，那么當k>1時將使得0多於1，這將導致矛盾。若同時存在0,1，那么這將使0,1交替出現，同樣導致矛盾。若只出現1，由泵引理知k可為0，而此時將有1不多於0，這也是矛盾的。因此該語言不是正則的。

例2：若為所有素數的二進制表示的0,1串，那么不是正則的。

證明：由初等數論易知存在任意大的素數，所以存在素數使得其二進制串長度大於泵引理閾值。將表示為，由泵引理知的二進制位串也屬於，因此也是素數。由費馬小定理知，所以即，又（即其可逆）所以。因此，所以| 這與為素數矛盾，故不是正則的。