在數論中，丟番圖逼近探討以有理數逼近實數的課題，逼近的程度通常以該有理數的分母衡量。
基本介紹
- 中文名：丟番圖逼近
- 外文名：Diophantine approximation
- 衡量方式：有理數的分母
- 目的：研究數的有理逼近問題
理論介紹,說明,相關介紹,
理論介紹
所謂丟番圖逼近即研究種種有理逼近的一個數論分支，因為它與丟番圖方程的研究密切相關，所以人們稱之為丟番圖逼近，或將這類問題稱為丟番圖分析。它還與幾何學有密切關係，為此，將設定數的幾何條目。中國古代對丟番圖逼近上很有貢獻的，例如，何承天與祖沖之就曾分別建議用22/7（約率）與355/113（密率）來近似計算圓周率π。這兩個數都是π都所謂漸近分數（見連分數）。355/113的下一個漸近分數為52163/16604，再下一個為103993/33102，太複雜了。因此，密率數是π極好的有理逼近。
說明
數論的一個分支，以研究數的有理逼近問題為主。這裡所謂的數是指實數、複數、代數數或超越數。數的有理逼近問題，可表為求某種不等式的整數解問題。由於在整數範圍求解的方程稱為不定方程或丟番圖方程，因而把求不等式的整數解問題稱之為丟番圖逼近。
1842年，P.G.L.狄利克雷首先證明了實數有理逼近的一個結果：如果α是任意實數，Q是大於1的實數，那么存在整數對p、q，滿足兩個不等式：
和
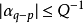。由此可得，如果α是任意無理數，那么存在無窮多對互素的整數對p、q，滿足不等式
。當α是有理數時，上式不成立。
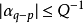
1891年，A.胡爾維茨將上式改進為
，並指出，對於某些無理數，常數
是最佳值，不可再減小。但是對於很多無理數，常數不是最佳值，還可再減小。
1926年，A.Я.辛欽證明了：在勒貝格測度意義下對幾乎所有的實數α，不等式
的整數解p、q有無窮多對還是只有有窮多對，由級數
是發散的還是收斂的而定，這裡 ψ(q)(q>0）是正的非增函式。此即所謂丟番圖逼近測度定理。例如，對幾乎所有的實數 α和任意的δ>0，不等式
只有有窮多對整數解，而不等式
有無窮多對整數解。
1844年，J.劉維爾開創了實代數數的有理逼近的研究，他證明了：如果α是次數為d的實代數數，那么存在一個常數C（α）>0，對於每個不等於α的有理數p/q，有
。亦即如果μ>d，那么不等式
只有有窮多個解
。根據這一結果，劉維爾構造出了歷史上的第一個超越數
。以後一些數學家不斷改進指數μ 的值，直到得出μ 與 d無關的結果。
1909年，A.圖埃得到
。
1921年，C.L.西格爾得到
。
1947年至1948年間，F.戴森和A.O.蓋爾豐德各自獨立證明了
。
1955年，K.F.羅特得到了μ與d無關的一個結論：如果α是實代數數，其次數 d≥2，那么對於任意的δ>0，不等式
只有有窮多個解。這一結論又稱為圖埃-西格爾-羅特定理。
用代數數逼近代數數，也是丟番圖逼近的一類重要內容。W.M.施密特所著《丟番圖逼近》（1980）一書中，有詳細的論述。
自20世紀以來，丟番圖逼近除自身的發展外，在超越數論、丟番圖方程等方面都有重要的套用。
相關介紹
劉維爾定理與 Roth 定理
劉維爾定理可用以直接構造超越數。在這之前，數學家們已藉連分數導出關於平方根與其它二次無理數的許多逼近性質。這個結果後來由 Axel Thue 等人改進，並導致 Roth 定理：將劉維爾定理中的指數 n 由代數數的次數縮減到任意的 2+ε（其中 ε>0）；之後 Schmidt 將此推廣到同步逼近。這些證明頗困難，而且不能得到明確的上界，這在套用上是一大缺憾。
均勻分布
取一實數序列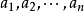
並考慮其真分數部份；或者抽象地說是考慮 R/Z，這在拓撲學上是個一維圓環 S1。對圓環上的任一段區間，我們研究有限集 {an:N<-N} 中有多大比例落在該區間，並考慮此比例與區間長度之關係。“均勻分布”意味著當 N→∞，此比例將趨近我們“期望”的值。Hermann Weyl 證明了這等價於該序列元素的指數和之上界，這表明了丟番圖逼近與指數和相消的一般問題密切相關，後者在解析數論的誤差項估計中無所不在。
其它面向
在 Roth 定理以後，丟番圖逼近的主要進展與超越理論相關。均勻分布關乎分布的不規則性，因而帶有組合學的本性。丟番圖逼近中仍有陳述簡單卻懸而未解的問題，例如勒特伍德猜想。
