基本介紹
存在性和描述,定義,形式上寫為,有關概念,證實 T 是包含 R 的最小傳遞關係,證明,推論,用途,與複雜性的關係,算法,Floyd-Warshall算法,核心代碼,
存在性和描述
定義
對於任何關係 R,R 的傳遞閉包總是存在的。傳遞關係的任何家族的交集也是傳遞的。進一步的,至少存在一個包含 R 的傳遞關係,也就是平凡的: X × X。R 傳遞閉包給出自包含 R 的所有傳遞關係的交集。
我們可以用更具體術語來描述 R 的傳遞閉包如下。定義在 X 上的一個關係 T,稱 xTy 若且唯若存在有限的元素(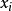 )序列,使得
)序列,使得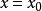 並且
並且
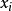
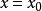
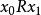
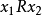
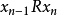
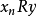
形式上寫為
容易檢查出關係 T 是傳遞的並且包含 R。進一步的,任何包含 R 的傳遞關係也包含 T,所以 T 是 R 的傳遞閉包。
有關概念
關係 R 的傳遞簡約是有 R 作為它的傳遞閉包的最小關係。一般的說它不是唯一的。
證實 T 是包含 R 的最小傳遞關係
證明
設 A 是任何元素的集合。
假定: GA 傳遞關係 RAGA TAGA。所以 (a,b)GA(a,b)TA. 所以,特定的 (a,b)RA。
現在通過 T 的定義,我們知道了 n (a,b)RnA。接著,i, in eiA。所以,有從 a 到 b 路徑如下: aRAe1RA...RAe(n-1)RAb。
但是,通過 GA 在 RA 上的傳遞性,i, in (a,ei)GA,所以,(a,e(n-1))GA (e(n-1),b)GA,所以通過 GA 的傳遞性,我們得到了 (a,b)GA。矛盾於 (a,b)GA。
因此,(a,b)AA, (a,b)TA (a,b)GA。這意味著 TG,對於任何包含 R 的傳遞的 G。所以,T 是包含 R 的最小傳遞閉包。
推論
如果 R 是傳遞的,則 R = T。
用途
注意兩個傳遞關係的並集不必須是傳遞的。為了保持傳遞性,必須採用傳遞閉包。例如,這出現在取兩個等價關係或預序的並的時候。為了獲得新的等價關係或預序,必須選用傳遞閉包(自反性和對稱性 — 在等價關係的情況下 — 是自動的)。
有向無環圖(DAG)的傳遞閉包是 DAG 的可到達性關係和一個嚴格偏序。
與複雜性的關係
在計算複雜性理論中,複雜度類 NL 嚴格對應於可使用一階邏輯和傳遞閉包表達的邏輯句子的集合。這是因為傳遞閉包性質有密切關係於 NL-完全問題 STCON,找到在一個圖中的有向路徑。類似的,類 L 是一階邏輯帶有交換傳遞閉包。在向二階邏輯增加了傳遞閉包的時候,我們得到 PSPACE。
算法
計算圖的傳遞閉包的有效算法可見於 here。最簡單的技術是Floyd-Warshall算法。
Floyd-Warshall算法
單獨一條邊的路徑也不一定是最佳路徑。 從任意一條單邊路徑開始。所有兩點之間的距離是邊的權的和,(如果兩點之間沒有邊相連, 則為無窮大)。 對於每一對頂點 u 和 v,看看是否存在一個頂點 w 使得從 u 到 w 再到 v 比己知的路徑更短。如果是更新它。 不可思議的是,只要按排適當,就能得到結果。// dist(i,j) 為從節點i到節點j的最短距離
For i←1to n do
For j←1to n do
dist(i,j) = weight(i,j)
For k←1to n do// k為“媒介節點”{一定要先枚舉媒介節點}
For i←1to n do
For j←1to n do
if(dist(i,k) + dist(k,j) < dist(i,j))then// 是否是更短的路徑?
dist(i,j) = dist(i,k) + dist(k,j)
這個算法的效率是O(V^3)。它需要鄰接矩陣來儲存圖。
這個算法很容易實現,只要幾行。
即使問題是求單源最短路徑,還是推薦使用這個算法,如果時間和空間允許(只要有放的下鄰接矩陣的空間,時間上就沒問題)。
核心代碼
for(k=0;k<g.vexnum;k++)
{
for(i=0;i<g.vexnum;i++)
{
for(j=0;j<g.vexnum;j++)
{
if(distance[i][j]>distance[i][k]+distance[k][j])
{
distance[i][j]=distance[i][k]+distance[k][j];
}
}
}
}
{
for(i=0;i<g.vexnum;i++)
{
for(j=0;j<g.vexnum;j++)
{
if(distance[i][j]>distance[i][k]+distance[k][j])
{
distance[i][j]=distance[i][k]+distance[k][j];
}
}
}
}

