沃舍爾算法

算法原理

本文嘗試對傳遞閉包的兩種算法（包含沃舍爾算法）進行描述，期間會用到路徑和0-1矩陣的表示方式。

詳解

1. 首先是從定義出發的標準算法，若要求出包含關係R的最小的傳遞閉包，我們就要為R中的每一種可能傳遞的關係補完其可傳遞性。不同於自反和對稱閉包，傳遞的複雜之處在於，他是可以有多重傳遞的，這就造成了初次補完R以後，新添加的關係有可能會和原有的關係一起產生新的傳遞關係（路徑），這時候就需要二次補完。同樣的道理，三次、四次...直到n次（n為R的頂點數）以後。

如上描述，求傳遞閉包的標準方法就是依次求出1、2、3...、n階傳遞關係並在每階求完之後與前一階的矩陣聯合，再進行下一階的求解。具體的操作方法是對原矩陣M_R（圖7-11右）進行布爾冪運算。我們可以看到——M_R^[k]的值m_ij正好是其前一階，即M_R^[k-1]的i行j列（或者說，頂點i和頂點j之間）傳遞關係存在與否的解。（難理解的話可以親手算一算）。

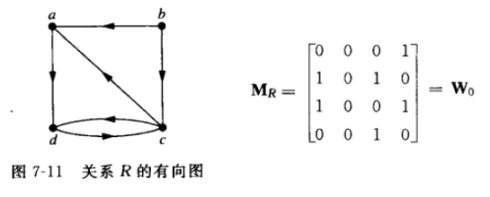
2. 接著是沃舍爾算法，這個算法比前面的標準算法複雜度上少了一階。沃舍爾算法使用了一條路徑的“內點”的概念。即如a，b，c，.....，x樣的一條路徑，除去a和x之外的所有端點稱為這條路徑的內點。具體的操作方法是以R為開頭構造一系列（n個）矩陣，他們是W₀ ,W₁,W₂,W₃,W₄ .....，其中W₀= M_R。這看起來和標準算法差不多，但是沃舍爾算法的高階矩陣的值並不是由前一階的布爾冪運算得來。而是這樣定義的：W_k=[w_ij^[k]]，如果存在一條從v_i到v_j的路徑且這條路徑的所有內點都在集合{v₁，v₂，....，v_k}（表中的前k個頂點）內，那么w_ij^[k]=1，否則為0.（注意有兩個合取的條件）。

可以看到，因為W_k-1中的“1”也必然滿足於W_k，所以W_k-1中的“1”可以直接繼承到W_k之中，即w_ij^[k-1]=1→w_ij^[k]=1。而對於W_k-1中的0，從前段的定義中我們可以看到，對於w_ij^[k-1]為0，而w_ij^[k]為1的情況，若且唯若w_ik^[k-1]=1且w_kj^[k-1]=1。（或者使用路徑的說法——存在一條從v_i到v_k和一條從v_k到v_j的路徑，使得當內點集合擴大到v_k時才滿足了前段定義的第二條條件）注意這裡的下標k，不再泛指k≤n的正整數，而是實指當前正在運算的W_k的k。舉圖7-11的例子來說明，W₁的w₂₄^[1]的值應該是w₂₁^[0]*w₁₄^[0]=1，而在W₀中這個位置的值是0.

總結來說，標準算法是通過n階布爾冪來化簡多重傳遞，並在過程中進行了矩陣合併的運算以保證所有路徑都被保留；而沃舍爾算法在每階矩陣的每個元素上，最多只進行2次布爾運算就可以取代標準算法的一個複雜度為O(n)的矩陣運算，因此效率得以提升。

程式

c++實現

#include <iostream>
#include <fstream>
#include <cstring>
using namespace std;
ifstream fin("data.txt");
ofstream fout("out.txt");
void in();
void out();
void solve();
int matri[20][20],n;
int main()
{
fin>>n;
memset(matri,0,sizeof(matri));
in();
solve();
out();
return 0;
}
void in()
{
int i,j;
for (i=1;i<=n;i++)
for (j=1;j<=n;j++)
fin>>matri[i][j];
return;
}
void out()
{
int i,j;
for (i=1;i<=n;i++)
{
for (j=1;j<=n;j++) fout<<matri[i][j]<<" ";
fout<<endl;
}
return;
}
void solve()
{
int k,i,j;
for (k=1;k<=n;k++)
for (i=1;i<=n;i++)
for (j=1;j<=n;j++)
{
if (matri[i][j]==1) continue;
if (matri[i][k]==1 && matri[k][j]==1) matri[i][j]=1;
}
}

沃舍爾算法

基本介紹

算法原理

詳解

程式

相關詞條

熱門詞條