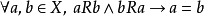反對稱關係

反對稱性是一個關於數學上二元關係的性質。大概地說，集合 X 上的二元關係 R 是反對稱的，若且唯若不存在X里的一對相異元素a, b，它們 R-關係於彼此。

基本介紹

• 中文名：反對稱關係
• 外文名：antisymmetric relation
• 領域：數學
• 性質：二元關係的性質
• 包括：偏序和全序

定義

更準確地說，集合 X 上的二元關係 R 是反對稱的，若且唯若對於X里的任意元素a, b，若a R-關係於 b 且 b R-關係於 a，則a=b。

用數學符號可寫成：

也可寫作，

或等價地，

例子

• 設X={1,2,3}，X上的兩個二元關係為R₁={(1,1),(1,2),(2,3),(3,1)}, R₂={(1,2),(2,1),(2,3),(3,1)}。R₁是反對稱的，R₂則不然。
  
• 實數集上的小於等於關係≤是反對稱的，如果有兩個實數x,y，x≤y且y≤x，則必有x=y。
  
• 設X為集合，則X的冪集P(X)上的子集關係⊆是反對稱的：設A, B為P(X)的元素，即A, B是X的子集。若A⊆B 且B⊆A，則A=B。
  
• 實數的嚴格小於關係<是反對稱的；實際上 a < b 且 b < a 是不可能的，因此嚴格不等的反對稱性是一種空虛的真（vacuously true）。
  
• 任意集合上的空關係（empty relation），即關係為空集時。
  
• 整數上的整除關係|不是反對稱的（因為1|-1，-1|1，但1≠-1）。如果限制在自然數範圍內則是反對稱的。
  
• 整數上的模n同餘是對稱的，但不是反對稱的。
  

性質

按照定義，偏序和全序都是反對稱的。

注意，反對稱關係不是對稱關係（aRb → bRa）的反義。有些關係既是對稱的又是反對稱的，比如"等於"。有些關係既不是對稱的也不是反對稱的，比如上面說的整除例子。

非對稱性（aRb∧~bRa）才算是對稱關係的反義。事實上，非對稱關係都符合反對稱性（vacuously）。非對稱關係亦即反對稱的非自反關係。（）。

一個n元素集上共有 個反對稱關係。

自反的、對稱的且可遷的關係稱為等價關係，自反的且可遷的關係稱為擬序關係，自反的、可遷的且反對稱的關係稱為序關係。