對應法則

對應法則（corresponding rule）是函式三大要素之一。一般地說，在函式記號y = f(x)中，“f”即表示對應法則，等式y = f(x)表明，對於定義域中的任意的x值，在對應法則“f”的作用下，即可得到值域中唯一y值。

基本介紹

• 中文名：對應法則
• 外文名：corresponding rule
• 套用學科：數學
• 適用領域範圍：高中函式
• 屬於：函式三大要素之一
• 表示方法：公式法、圖像法、列表法

定義

函式概念的核心是變數y與變數x之間的對應法則。表示這種對應法則的方法是多種多樣的，通常有公式法、圖象法及列表法。但為了對函式進行一般性的研究，我們用記號 y=f(x)表示變數y是變數x的函式，其中字母“f”就抽象地表示變數y與變數x的對應法則。

簡單地說，自變數x可通過方法f（所謂對應法則）“變成”了因變數y。

因此，“f”是使“對應”得以實現的方法和途徑，是聯繫x與y的紐帶，從而也就是函式的核心。

可以用一句話、一張圖表、也可以是一個解析式表示。

特別地，f(a)表示自變數x=a時所得的函式值，是一個常量；而f(x)稱為變數x的函式，在通常情況下，它是一個變數。

舉例說明

例如，在函式式

中對應法則f這時相當於運算程式

按照這樣的運算程式，對指定的定義域[-1,2)∪(2,9]中的x值，可計算出對應的y值。比如，取x=-1，對應的y值為

又比如，取x=8，對應的y值為

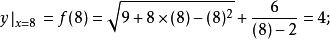
當x=2時，y沒有對應值，或說函式y=f(x)在點x=2處沒有定義。可以知道f(x)在點x=-2處也沒有定義，但應注意兩者有明顯的區別，主要是：存在一個以x=2為中心的去心領域，比如0<|x-2|<2，在該領域內f(x)有定義；而存在一個以x=-2為中心的領域，比如|x+2|<1，在該領域內f(x)卻處處無定義。

一般地，設函式y=f(x)的定義域為D，則對於任一數x₀∈D，所對應的y值記為或f(x₀)，並稱之為函式y=f(x)在點x₀處的函式值。有時，也用f(x)本身來表示D中任一點x處的函式值。

定義域D中的一切x值所對應的全體函式值的集合E叫做函式的值域。即稱數集

為函式y=f(x)（x∈D）的值域。

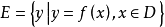
套用

在確定兩個函式是否為同一函式時，定義域和值域都相同不一定就是同一函式，對應法則f為關鍵要素。

可以運用化學的知識理解y相當於生成物，f相當於反應條件或者是催化劑把反應物x變為y。

由函式奇偶性的定義我們知道，判斷函式的奇偶性，首先，應看其定義域是否關於原點對稱，其次，需判斷f(x)與f(-x)的關係，而f(x)與f(-x)的關係離不開對應法則的套用。奇偶性的判別方法，可歸納為3種：①利用奇偶性的定義；②用和差判別法，即考察f(-x)±f(x)與0的關係；③用求商判別法，即考察f(-x)/f(x)與±1的關係。