基本介紹
- 中文名:代數式
- 外文名:algebraic expression
- 類型:數學名詞
- 連線:運算符號
簡介

注意事項





發展
分類
有理式
無理式
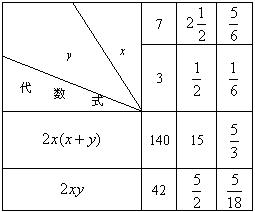 圖1.
圖1.書寫格式
數式的運算
產生
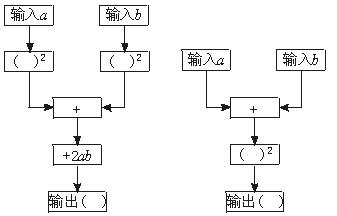 代數式
代數式






 圖1.
圖1. 代數式
代數式由數和表示數的字母經有限次加、減、乘、除、乘方和開方等代數運算所得的式子,或含有字母的數學表達式稱為代數式。例如:ax+2b,-2/3,b^2/26,√a+√2等。...
代數是研究數字和文字的代數運算理論和方法,更確切的說,是研究實數和複數,以及以它們為係數的多項式的代數運算理論和方法的數學分支學科。“代數”作為一個數學專有...
用數值代表代數式里的字母,按照代數式中的運算關係計算得出的結果叫做代數式的值。...... 用數值代表代數式里的字母,按照代數式中的運算關係計算得出的結果叫做代數...
列代數式:把問題中與數量有關的詞語,用含有數字、字母和運算符號的式子表示出來,就是列代數式。列代數式對解方程很有幫助。...
代數方程,即由多項式組成的方程。有時也泛指由未知數的代數式所組成的方程,包括整式方程、分式方程和根式方程。例如:5x+2=7,x=1等。 代數,把algebra翻譯成代數...
如果兩個代數式A和B,對於它們中字母在允許範圍內任意取值,它們都有相同的值,那么就說這兩個代數式恆等。...
代數是研究數、數量、關係、結構與代數方程(組)的通用解法及其性質的數學分支。初等代數一般在中學時講授,介紹代數的基本思想:研究當我們對數字作加法或乘法時會發生...
在n階行列式中,把元素aₒₑi所在的第o行和第e列划去後,留下來的n-1階行列式叫做元素aₒₑi的餘子式,記作Mₒₑ,將餘子式Mₒₑ再乘以-1的...
設A,B,D是集合,稱A×B到D的映射為A×B到D的代數運算。如有n元函式f:S1×S2×...×Sn→S中有S=S1=S2=...=Sn則稱f 為S 上的n 元代數運算,或...
代數學基本定理:任何復係數一元n次多項式 方程在複數域上至少有一根(n≥1),由此推出,n次復係數多項式方程在複數域內有且只有n個根(重根按重數計算)。代數基本...
邏輯代數是一種用於描述客觀事物邏輯關係的數學方法,由英國科學家喬治·布爾(George·Boole)於19世紀中葉提出,因而又稱布爾代數。邏輯代數有一套完整的運算規則,包括...
關係代數是一種抽象的查詢語言,用對關係的運算來表達查詢,作為研究關係數據語言的數學工具。關係代數的運算對象是關係,運算結果亦為關係。關係代數用到的運算符包括...
如果代數式中含有表達式的開方運算,而表達式中又含有字母,則此代數式就叫做這些字母的無理代數式,簡稱無理式(irrational expression)。無理式與無理數(irrational ...
一般地,如果A、B(B不等於零)表示兩個整式,且B中含有字母,那么式子A / B 就叫做分式,其中A稱為分子,B稱為分母。分式是不同於整式的一類代數式,分式的值隨...
由數或字母的積組成的代數式叫做單項式,單獨的一個數或一個字母也叫做單項式(例:0可看做0乘a,1可以看做1乘指數為0的字母,b可以看做b乘1),分數和字母的積...
一般地,形如√a的代數式叫做二次根式,其中,a 叫做被開方數。當a≥0時,√a表示a的算術平方根;當a小於0時,√a的值為純虛數(在一元二次方程求根公式中,若...
式子,指算式、代數式、方程式等的統稱。姿勢可以是一種學術用語,也可以是一個漢語辭彙。...
根式是數學的基本概念之一,是一種含有開方(求方根)運算的代數式,即含有根號的表達式。按根指數是偶數還是奇數,根式分別稱為偶次根式或奇次根式。...
解析式是代數學的基本概念之一。用運算符號和括弧把數字和字母按一定規則連結成的式子稱為解析式,常簡稱式。解析式分為代數式和超越式兩大類。...
在數學中,算式(suàn shì)是指在進行數(或代數式)的計算時所列出的式子,包括數(或代替數的字母)和運算符號(四則運算、乘方、開方、階乘、排列組合等)兩部分...
在數學中,由若干個單項式相加組成的代數式叫做多項式(若有減法:減一個數等於加上它的相反數)。多項式中的每個單項式叫做多項式的項,這些單項式中的最高項次數,就...
