基本介紹
- 中文名:代數運算
- 外文名:Algebraic operation
- 屬性:數學術語
代數運算的意義





運算律
結合律


交換律


消去律

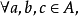



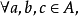




分配律


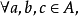








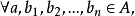
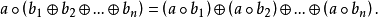


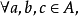
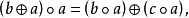







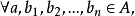
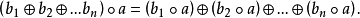
例題分析


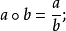

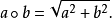





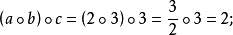
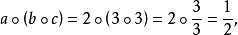

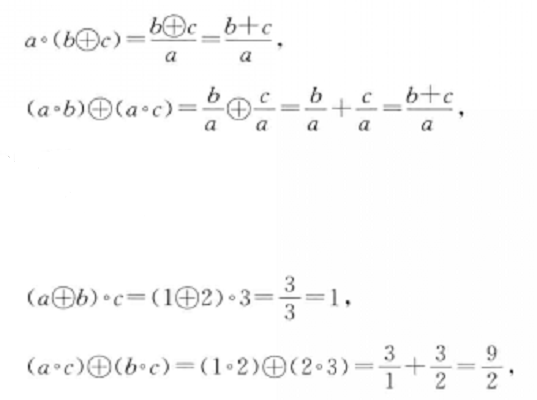










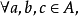



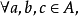






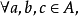








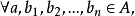
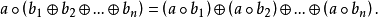


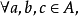
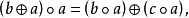







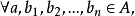
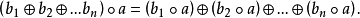


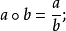

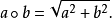





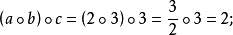
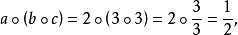

設A,B,D是集合,稱A×B到D的映射為A×B到D的代數運算。如有n元函式f:S1×S2×...×Sn→S中有S=S1=S2=...=Sn則稱f 為S 上的n 元代數運算,或...
由數和表示數的字母經有限次加、減、乘、除、乘方和開方等代數運算所得的式子,或含有字母的數學表達式稱為代數式。例如:ax+2b,-2/3,b^2/26,√a+√2等。...
代數是研究數、數量、關係、結構與代數方程(組)的通用解法及其性質的數學分支。初等代數一般在中學時講授,介紹代數的基本思想:研究當我們對數字作加法或乘法時會發生...
代數數是代數與數論中的重要概念,指任何整係數多項式的復根。所有代數數的集合構成一個域,稱為代數數域。不是代數數的實數稱為超越數,例如圓周率。...
關係代數是一種抽象的查詢語言,用對關係的運算來表達查詢,作為研究關係數據語言的數學工具。關係代數的運算對象是關係,運算結果亦為關係。關係代數用到的運算符包括...
運算,數學上,運算是一種行為,通過已知量的可能的組合,獲得新的量。運算的本質是集合之間的映射。一般說來,運算都指代數運算,它是集合中的一種對應。對於集合A中...
《代數計算器》是一款Android平台的套用。...... 代數是研究數字和文字的代數運算理論和方法,更確切的說,是研究實數和複數,以及以它們為係數的多項式的代數運算理論...
基本運算是指執行運算最基礎的算法。在關係代數運算中,有5種基本運算,它們是並(U)、差(—)、投影、選擇、笛卡爾積(X),其它運算即交、連線和除,均可通過5種...
代數和是指兩個或更多的數或量按照代數加法規律取符號(如 +或-)的總和。...... 代數計算中,可以省略括弧和括弧前的“+”號,可以有兩種讀法。一種是直接讀出省...
集合代數發展並描述了集合的基本性質和規律,集合論運算,如並集、交集、補集,以及集合的關係,如等於、包含。這門學科系統研究如何來表達和進行上述的運算和關係的操作...
代數方程,即由多項式組成的方程。有時也泛指由未知數的代數式所組成的方程,包括整式方程、分式方程和根式方程。例如:5x+2=7,x=1等。 代數,把algebra翻譯成代數...
代數是研究數字和文字的代數運算理論和方法,更確切的說,是研究實數和複數,以及以它們為係數的多項式的代數運算理論和方法的數學分支學科。“代數”作為一個數學專有...
代數是研究數、數量、關係、結構與代數方程(組)的通用解法及其性質的數學分支。初等代數一般在中學時講授,介紹代數的基本思想:研究當我們對數字作加法或乘法時會發生...
初等代數(elementary algebra)是研究數字和文字的代數運算理論和方法,更確切的說,是研究實數和複數,以及以它們為係數的代數式的代數運算理論和方法的數學分支學科。...
布爾代數的運算律(operational rule of Boolean algebra)是布爾代數的基本運算法則,布爾代數中的變數代表一種狀態或概念,數值1或0並不是表示變數在數值上的差別而是...
代數學基本定理:任何復係數一元n次多項式 方程在複數域上至少有一根(n≥1),由此推出,n次復係數多項式方程在複數域內有且只有n個根(重根按重數計算)。代數基本...
關係的基本運算有兩類:一類是傳統的集合運算(並、差、交等),另一類是專門的關係運算(選擇、投影、連線、除法、外連線等),有些查詢需要幾個基本運算的組合,要...
運算律是通過對一些等式的觀察、比較和分析而抽象、概括出來的運算規律。既是重要的數學規律,也是數學運算固有的性質。包括加法交換律和結合律、乘法交換律和結合律...
二元運算是由兩個元素形成第三個元素的一種規則。例如數的加法及乘法;更一般地,由兩個集合形成第三個集合的產生方法或構成規則稱為二次運算。二元運算(Binary ...
用數值代表代數式里的字母,按照代數式中的運算關係計算得出的結果叫做代數式的值。...... 用數值代表代數式里的字母,按照代數式中的運算關係計算得出的結果叫做代數...
