陪域(Codomain)又稱上域、到達域。設G是從X到Y的關係,G的定義域D(G)為X,且對任何x∈X都有惟一的y∈Y滿足G(x,y),則稱G為從X到Y的映射。關係G常使用另一些記號:f:X→Y等,f與G的關係是y=f(x)(x∈X),若且唯若G(x,y)成立,可取變域X中的不同元素為值的變元稱為自變元或自變數,同樣可取變域Y中的不同元素為值的變元稱為因變元或因變數。始集X稱為映射f的定義域,記為D(f)或dom(f);終集Y稱為映射的陪域,記為C(f)或codom(f);Y中與X中的元素有關係G的元素的組合{y|∃x(x∈X∧y=f(x)∈Y)}稱為映射的值域,記為R(f)或ran(f);當y=f(x)時,y稱為x的象,而x稱為y的原象,y的所有原象所成之集用f-1(y)表示;對於A⊆X,所有A中元素的象的集合{y|∃x(x∈A∧y=f(x)∈Y)}或{f(x)|x∈A}稱為A的象,記為f(A);對於B⊆Y,所有B中元素的原象的集合{x|x∈X∧∃y(y∈B∧y=f(x))}稱為B的原象,記為f-1(B)。
基本介紹
- 中文名:陪域
- 外文名:Codomain
- 別稱:上域
- 所屬學科:數學
- 相關概念:值域,定義域,象,原象等
基本介紹



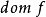
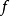



單射、滿射與雙射
 圖1雙射(單射與滿射) |  圖2 單射但非滿射 |
 圖3 滿射但非單射 |  圖4 非滿射非單射 |
單射
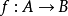
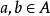

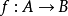

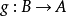

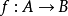
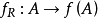


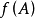



 圖5 單射複合:第二個函式不必是單射
圖5 單射複合:第二個函式不必是單射滿射
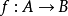


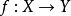
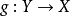






 圖6 滿射複合:第一個函式不必為滿射
圖6 滿射複合:第一個函式不必為滿射雙射
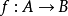


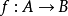

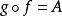

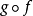
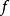

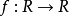
 圖7 雙射複合:第-個函式不必為滿射、第二個函式不必為單射
圖7 雙射複合:第-個函式不必為滿射、第二個函式不必為單射
定義域 | 陪域 | 映射 | 單射 | 滿射 | 雙射 |
R | 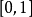 | × | × | × | × |
R | R | √ | × | × | × |
R | 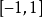 | √ | × | √ | × |
 | R | √ | √ | × | × |
 | 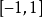 | √ | √ | √ | √ |

