到達域(英語:codomain),或稱為陪域、上域、靶(英語:target set)。
基本介紹
- 中文名:到達域
- 分類:數理科學
定義
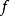
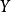
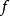
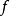
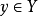
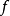
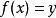
例
例一
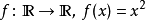
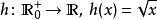
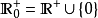
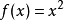
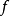
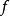
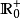
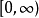
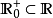
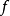
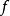
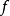
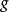
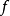
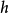

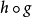
例二

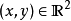
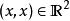
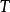
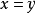
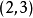
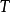
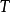
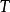
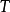
到達域(英語:codomain),或稱為陪域、上域、靶(英語:target set)。
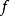
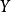
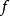
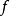
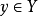
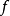
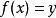
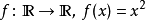
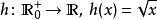
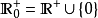
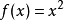
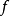
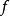
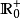
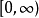
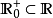
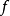
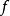
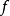
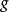
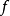
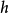

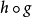

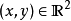
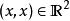
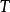
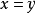
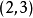
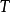
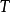
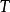
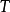
到達域(英語:codomain),或稱為陪域、上域、靶(英語:target set)。...... 在數學領域中,一個函式的到達域指的是至少包含所有此函式的輸出值的一個集合。在函式...
到達船舶,是指到達航次租船契約約定的港口或泊位的船舶。起算裝卸時間的條件之一。如果契約是一個“港口契約”,船舶到達契約指定的港口視作到達船舶,港口範圍一般指...
到達網路是一家專業從事網站建設、網路行銷的公司,總部位於美麗的海濱城市山東煙臺。到達網路包括一支由網路行銷顧問、網路行銷技術工程師、網站設計美工、網路客服組成...
只要出發,就能到達編輯 鎖定 黑天鵝圖書出品,中國華僑出版社出版。美國版《誰的青春不迷茫》,一位美國草根的成功之路,寫給夢想很多,卻還沒有找到一條成功之路的你...
在一定區域內特定的某個廣告通過聲音、影像或者實體物可以讓此區域內聽到、看到此廣告的人數除以此區域內的總人數;廣告到達率也廣泛套用於網路廣告,到達率是指瀏覽...
陪域(Codomain)又稱上域、到達域。設G是從X到Y的關係,G的定義域D(G)為X,且對任何x∈X都有惟一的y∈Y滿足G(x,y),則稱G為從X到Y的映射。關係G常使用...
廣州捷運三號線北延段南起天河區體育西路站,經林和西、廣州東、燕塘、梅花園、京溪南方醫院、同和、永泰、嘉禾、龍歸、人和站後到達機場南站(1號航站樓)和機場...
區域減肥法如何到達區域? 編輯 席爾斯說吃東西必須緩慢,而且有一定的比例,「宛如靜脈注射」,他設定一個包括碳水化合物、蛋白質和脂肪的系統,你可以分配到一天三餐和...
第三十一章 到達域外 第三十二章 吞噬世界 第三十三章 道心動猴王出海 第三十四章 異界來客 第三十五章 意外被抓 第三十六章 萬神大世界(一) 第三十七...
市域鐵路:又稱為通勤鐵路、市郊鐵路,指的是大都市市域範圍內的客運軌道交通系統,服務於城市與郊區、中心城市與衛星城、重點城鎮間等,服務範圍一般在50---100...
小說類型異術異能內容簡介千虛 一個小矮子 誰知道他的身世?沒人 流浪在源樂域與源罪域之間 當情緒到達極點時 他的性格分裂開來 一股神秘的力量由此產生 詭異而又...
中國域,作者衝出第一島鏈,連載網站幻俠小說...... 中國域,作者衝出第一島鏈,連載網站幻俠小說 ...到達了xìng yù制高點後的王若欣極為舒服地叫聲連連…...
