函式的有界性定義:若存在兩個常數m和M,使函式y=f(x),x∈D 滿足m≤f(x)≤M,x∈D 。 則稱函式y=f(x)在D有界,其中m是它的下界,M是它的上界。
基本介紹
- 中文名:有界性
- 外文名:boundedness
- 所屬學科:數理科學函式
- 分類:上界、下界
- 相關概念:有界、無界、
定義
定義1
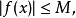
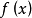
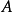
定義2

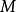
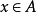
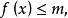

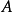

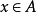
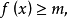

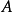

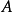




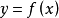
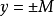
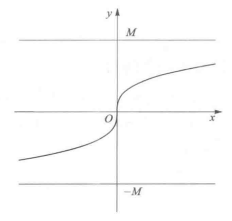 圖1
圖1注意點
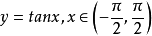
 圖2
圖2例題解析
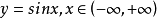
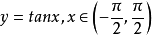

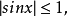
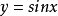
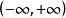
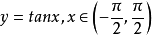
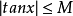
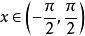
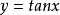
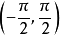
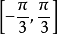
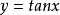
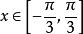
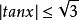
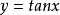
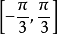
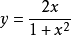
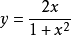
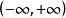
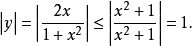
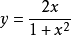

函式的有界性定義:若存在兩個常數m和M,使函式y=f(x),x∈D 滿足m≤f(x)≤M,x∈D 。 則稱函式y=f(x)在D有界,其中m是它的下界,M是它的上界。
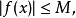
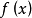
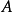

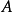
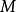
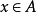
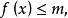

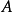

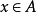
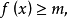

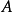

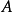




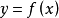
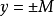
 圖1
圖1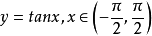
 圖2
圖2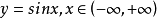
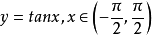

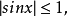
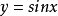
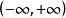
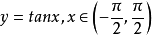
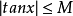
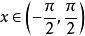
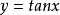
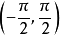
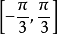
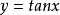
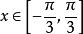
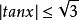
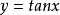
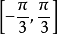
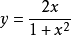
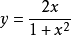
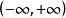
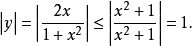
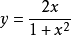
函式的有界性定義:若存在兩個常數m和M,使函式y=f(x),x∈D 滿足m≤f(x)≤M,x∈D 。 則稱函式y=f(x)在D有界,其中m是它的下界,M是它的上界。...
在極限理論中,我們知道閉區間上連續函式具有5個性質,即:有界性定理、最大值與最小值定理、介值定理、零點定理和一致連續性定理。其中,零點定理是介值定理的一個...
函式的有界性是數學術語。設函式f(x)的定義域為D,f(x)在集合D上有定義。如果存在數K1,使得 f(x)≤K1對任意x∈D都成立,則稱函式f(x)在D上有上界。反...
擬微分運算元有界性(boundedness of pseu-dodifferential operators)擬微分運算元在某些函式空間上所滿足的範數關係.在諸如索伯列夫空間、赫爾德空間及別索夫空間等重要的...
有界n線性運算元是映有界集的n線性運算元。n線性運算元的有界性與連續性是等價的。...... 有界n線性運算元是映有界集的n線性運算元。n線性運算元的有界性與連續性是等價...
概念定義 L2有界性定理(I2-boundedness theorem)擬微分運算元的重要性質.設AEOP娜,s(,(2) , OGBGpG 1,且K,具緊支集,則A可延拓為1 Z(})-}1 Z(,(})...
並且一個有序域被稱為完全的,如果它的任何在這個域中有上界的非空子集,都有一個在這個域中的最小上界;注意這個定義與序理論中的完全有界性(bounded complete)...
第二章研究帶禁止類的雙線性擬微分運算元,我們證明了帶禁止類的雙線性擬微分運算元在Morrey型Sobolev空間及Morrey型Besov空間上的有界性.類似地,得到了此類運算元在Herz型...
主要包括三個部分:Banach空間微分學(連續、有界、導數、全連續、微分方程與Hamiltoin系統的變分學框架、隱函式定理、分歧與約化)拓撲度及錐理論(Brouwer度、L-S...
零性向量雙線性泛函 編輯 設A是H上的線性運算元,則稱φ(x,y)=(Ax,y)為由運算元A導出的雙線性泛函。希爾伯特空間上的有界雙線性泛函必是H上的有界線性運算元導出...
8.3 有界線性泛函的超限閉集8.4 有界線性?函的弱收斂性8.5 可分Banach空間中有界線性泛函的弱閉集8.6 空間C,L,c和l中的有界線性泛函的弱收斂性條件...
),則“隨機點X落在點x左邊”這一事件趨於必然事件,從而趨於機率1,即有 [2] 分布函式3右連續性 (3) ;證明:因為 F(x)是單調有界非減函式,所以其任一點x...
在泛函分析中,它定義在賦范線性空間中,並滿足一定的條件,即①非負性;②齊次...如,在常用的範數下,積分運算元是有界的,微分運算元是無界的。容易證明,有限維空間...
卡普蘭斯基稠密性定理是關於C*代數的單位球在它生成的馮·諾伊曼代數的單位球中稠密的定理。卡普蘭斯基稠密性定理斷言:若𝓐是希爾伯特空間H上有界線性運算元全體𝓑(...
描述系統動力學特性的微分方程之右端是一個函式,由該函式值的大小可判定方程解的大小,從而可用於判別系統運動的有界性和穩定性。中文名 比較原理 外文名 ...
①有界性②單調性 單調函式 ③奇偶性④周期性公式一:設α為任意角,終邊相同的角的同一三角函式的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosα...
2.了解函式的有界性、單調性、周期性和奇偶性. 3.理解複合函式及分段函式的概念,了解反函式及隱函式的概念. 4.掌握基本初等函式的性質及其圖形,了解初等函式的概...
9. VP的有界性與連動式的事件結構,現代外語,2013.2,第二作者。 [1] 10. 類型邏輯語法與漢語中的照應省略,湖南科技大學學報(社會科學版),2011.2(人大複印...
3.存在某個復賦范線性空間上的可加連續運算元,它不滿足復齊性的條件 4.l∞上的一個有界線性泛函f,不能表成f(x)=∑n=1∞βnξn的形式,其中x={ξn}∈...
