在頻域中的乘積運算元或在時域中的卷積運算元在Hankel和特普利茨(Toeplitz)運算元的發展中扮演了一個重要的角色。事實上,乘積運算元可分解成若干Hankel和特普利茨(Toeplitz)運算元。
基本介紹
- 中文名:特普利茨運算元
- 外文名:Toeplitz operator
- 套用學科:數學術語
- 範疇:數理科學
- 涉及:Hardy空間
- 又稱:Toeplitz運算元
概念
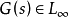

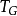




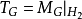




基本原理



























在頻域中的乘積運算元或在時域中的卷積運算元在Hankel和特普利茨(Toeplitz)運算元的發展中扮演了一個重要的角色。事實上,乘積運算元可分解成若干Hankel和特普利茨(Toeplitz)運算元。
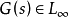

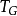




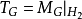






























在頻域中的乘積運算元或在時域中的卷積運算元在Hankel和特普利茨(Toeplitz)運算元的發展中扮演了一個重要的角色。事實上,乘積運算元可分解成若干Hankel和特普利茨(Toeplitz)...
特普利茨運算元是一類函式空間運算元,是運算元理論的重要研究對象之一。...... 特普利茨矩陣特普利茨運算元 特普利茨運算元是一類函式空間運算元,是運算元理論的重要研究對象之一。...
特普利茨方程是一類理論上重要的奇異積分方程.設已給函式a(t)EL00,t定義在單位圓周上。...
簡介特普利茨(Toeplitz, Otto,1881-1940)德國數學家,生於德國布雷斯勞,早年在布雷斯勞大學學習,1905年獲博士學位.先後在格廷根大學、基爾大學、波恩大學工作.1938年,...
黑林格-特普利茨定理是數學泛函分析的定理,以德國數學家恩斯特·黑林格和奧托·特普利茨命名。...
特普利茨代數是一種具體的C*代數,是C*代數理論和運算元理論的重要研究對象。...... 特普利茨代數是一種具體的C*代數,是C*代數理論和運算元理論的重要研究對象。...
5.設函式a(t)EL00(}t}=1),運算元Arp =a(t>抓t > , }p屬於哈代空間Hp , P是1”到H”的投影運算元,已知函式fEH',則特普利茨方程可記為 Tp}a}} = ...
在此基礎上,施密茨、赫林格和特普利茨發展出運算元理論,而無限維矩陣成為了研究函式空間運算元的有力工具 [7] 。矩陣的概念最早在1922年見於中文。1922年,程廷熙在一篇...
共鳴定理亦稱一致有界性原理或巴拿赫-施坦豪斯定理,是論述有關一族有界線性運算元...關於奇異積分、特普利茨(Toeplitz,O.)關於正則求和法以及哈恩(Hahn,H.) 關於...
