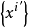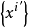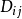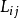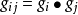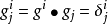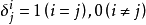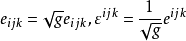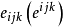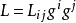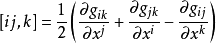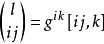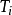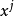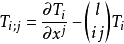張量（tensor）理論是數學的一個分支學科，在力學中有重要套用。張量這一術語起源於力學，它最初是用來表示彈性介質中各點應力狀態的，後來張量理論發展成為力學和物理學的一個有力的數學工具。張量之所以重要，在於它可以滿足一切物理定律必須與坐標系的選擇無關的特性。張量概念是矢量概念的推廣，矢量是一階張量。張量是一個可用來表示在一些矢量、標量和其他張量之間的線性關係的多線性函式。
基本介紹
- 中文名：張量
- 外文名：Tensor
- 提出者：威廉·羅恩·哈密頓
- 提出時間：1846年
- 套用學科：力學，數學
- 適用領域範圍：連續介質力學
物理名稱,背景知識,規定,定義,基本運算,特殊張量,協變導數與算符,例子,張量密度,張量相關,
物理名稱
張量（Tensor）是一個定義在一些向量空間和一些對偶空間的笛卡兒積上的多重線性映射，其坐標是|n|維空間內，有|n|個分量的一種量， 其中每個分量都是坐標的函式， 而在坐標變換時，這些分量也依照某些規則作線性變換。r 稱為該張量的秩或階（與矩陣的秩和階均無關係）。
在同構的意義下，第零階張量 （r = 0） 為標量 （Scalar），第一階張量 （r = 1） 為向量 （Vector）， 第二階張量 （r = 2） 則成為矩陣 （Matrix）。例如，對於3維空間，r=1時的張量為此向量：（x,y,z）。由於變換方式的不同，張量分成協變張量 （Covariant Tensor，指標在下者）、逆變張量 （Contravariant Tensor，指標在上者）、 混合張量 （指標在上和指標在下兩者都有） 三類。
在數學里，張量是一種幾何實體，或者說廣義上的“數量”。張量概念包括標量、向量和線性運算元。張量可以用坐標系統來表達，記作標量的數組，但它是定義為“不依賴於參照系的選擇的”。張量在物理和工程學中很重要。例如在擴散張量成像中，表達器官對於水的在各個方向的微分透性的張量可以用來產生大腦的掃描圖。可能最重要的工程上的例子就是應力張量和應變張量了，它們都是二階張量，對於一般線性材料他們之間的關係由一個四階彈性張量來決定。
雖然張量可以用分量的多維數組來表示，張量理論存在的意義在於進一步說明把一個數量稱為張量的涵義，而不僅僅是說它需要一定數量的有指標索引的分量。特別是，在坐標轉換時，張量的分量值遵守一定的變換法則。張量的抽象理論是線性代數分支，現在叫做多重線性代數。
背景知識
這個概念由格雷戈里奧·里奇-庫爾巴斯特羅在1890年在《絕對微分幾何》的標題下發展出來，隨著1900年列維-奇維塔的經典文章《絕對微分》（義大利文，隨後出版了其他譯本）的出版而為許多數學家所知。隨著1915年左右愛因斯坦的廣義相對論的引入，張量微積分獲得了更廣泛的承認。廣義相對論完全由張量語言表述，愛因斯坦從列維-奇維塔本人那裡學了很多張量語言（其實是Marcel Grossman,他是愛因斯坦在蘇黎世聯邦理工學院的同學，一個幾何學家，也是愛因斯坦在張量語言方面的良師益友 - 參看Abraham Pais所著《上帝是微妙的（Subtle is the Lord）》），並學得很艱苦。但張量也用於其它領域，例如連續力學，譬如應變張量（參看線性彈性）。
規定
1.求和約定
指在給定的項中凡有一上和一下兩個相同的指標就表示對該指標從1到空間維數N求和。例如，在三維空間中，
2.張量指標
包括啞指標和自由指標。啞指標是指各項中一上和一下成對的相同指標。例如，上式中的指標i就是啞指標。自由指標是指在方程的所有項中只出現一次的指標。
定義
有兩種定義張量的方法：
1. 按變換規律定義
若一坐標系
中
個量
與另一坐標系
中 個量
間滿足交換規律
則 稱為r階逆變和s階協變混合張量的分量。若s=0，則
稱為r階逆變張量的分量。若r=0，則
稱為s階協變張量的分量。上述這種張量記法稱為分量記法。
2.按不變性定義
凡可以在任何坐標系中寫成下列不變性形式的量定義為r+s階張量：
基本運算
1． 加減法
兩個或多個同階同型張量之和（差）仍是與它們同階同型的張量。
2． 並積
兩個張量的並積是一個階數等於原來兩個張量階數之和的新張量。
3． 縮並
使張量的一個上標和一個下標相同的運算，其結果是一個比原來張量低二階的新張量。
4． 點積
兩個張量之間並積和縮並的聯合運算。例如，在極分解定理中，三個二階張量R、U和V中一次點積R·U和V·R的結果是二階張量F。
5． 對稱化和反稱化
對已給張量的n個指標進行n1不同置換並取所得的n1個新張量的算術平均值的運算稱為對稱化。把指標經過奇次置換的新張量取反符號後再求算術平均值的運算稱為反稱化。
6． 加法分解
任意二階張量可以唯一地分解為對稱部分和反稱部分之和。例如，速度梯度
可以分解為
，其中
和
分別為
的對稱和反稱部分，即
和
。
1． 商法則
肯定某些量的張量性的法則。
特殊張量
特殊張量主要有四種：
①度量張量 兩個基矢量點積的結果。
和
分別稱為協變和逆變度量張量，而混合度量張量
，這裡
（或寫為
）為克羅內克符號，它定義為：
②交錯張量或愛丁頓張量 可定義為
，這裡
表示元素
為行列式，而置換符號
表示
（
是(1,2,3)的偶次置換），-1（ 是(1,2,3)的奇次置換），0（其餘情形）
③轉置張量 對任意二階張量
的分量指標置換的結果，記為
。
④正交張量 保持映象長度不變的二階張量。
克里斯機費爾符號 第一類和第二類克里斯托費爾符號分別定義為：
和
。
協變導數與算符
1.協變導數
協變矢量
和逆變矢量
關於
的協變導數分別定義為：
和
。上列結果可以推廣到高階張量的協變導數。
2.不變性微分算符
推廣矢量分析概念，對於任意張量場T有四種不變性微分算符，即梯度▽T，散度▽·T，旋度▽×T和拉普拉斯算符▽2T。
在直角坐標系下，協變和逆變間的差別消失，故可規定所有指標均寫成下標，另外，由於克里斯托費爾符號為零，所以協變導數變成為普通偏導數。
例子
張量可以表述為一個值的序列，用一個向量值的定義域和一個標量值的值域的函式表示。這些定義域中的向量是自然數的向量，而這些數字稱為指標。例如，3階張量可以有尺寸2、5和7。這裡，指標的範圍是從<1,1,1,>到<2,5,7>。張量可以在指標為<1,1,1>有一個值，在指標為<1,1,2>有另一個值，等等一共70個值。（類似的，向量可以表示為一個值的序列，用一個標量值的定義域和一個標量值的值域的函式表示，定義域中的數字是自然數，稱為指標，不同的指標的個數有時稱為向量的維度。）
一個張量場是在歐幾里得空間中的每一點都給定一個張量值。這樣不是像上面的例子中簡單的有70個值，對於一個3階張量，維度為<2,5,7>，空間中的每一個點有70個值和它相關。換句話說，張量場表示某個張量值的函式，其定義域為歐幾里得空間。不是所有的函式都行 -- 更多關於這些要求的細節參看張量場。
不是所有自然中的關係都是線性的，但是很多是可微的因而可以局部的用多線性映射來局部的逼近。這樣多數物理學中的量都可以用張量表示。
作為一個簡單的例子，考慮水中的船。我們要描述它對受力的反應。力是一個向量，而船的反應是一個加速度，它也是一個向量。通常加速度不是和受力的方向相同，因為船體的特定形狀。但是，這個力和加速之間的關係實際上是線性的。這樣一個關係可以用一個（1,1）類型（也就是說，它把一個向量變成另一個向量）的張量表示。這個張量可以用矩陣表示，當它乘以一個向量時就得到另一個作為結果。坐標系改變的時候，表示一個向量的數字會改變，同樣，表示這個張量的矩陣中的數字也會改變。
實際上，張量的概念相當廣泛，可以用於上面所有的例子；標量和向量是張量的特殊情況。區別標量和向量以及區別這兩者和更一般的張量的特徵是表示它們的數組的指標的個數。這個數稱為張量的階。這樣，標量是0階張量（不需要任何指標），而向量是一階張量。
張量的另外一個例子是廣義相對論中的黎曼曲率張量，它是維度為<4,4,4,4>（3個空間維度 + 時間維度 = 4個維度）的4階張量。它可以當作256個分量（256 = 4 × 4 × 4 × 4）的矩陣（或者向量，其實是個4維數組）。只有20個分量是互相獨立的，這個事實可以大大簡化它的實際表達。
張量密度
張量場也可有一個“密度”。密度為 r 的張量和普通張量一樣坐標變換，但是它還要乘以雅可比矩陣的行列式值的第 r 次冪。這個的最佳解釋可能是使用向量叢：其中，切叢的行列式叢是一個線叢，可以用來'扭轉'其它叢 r 次。
張量相關
1.張量的理論來源。
亞瑟·凱萊( Arthur Cayley)著力研究的不變數理論( invariant theory)導致了矩陣理論的建立，引進了現代意義上的行列式的代數表達,這成為射影幾何的重要工具。凱萊的不變數理論產生於19世紀前半葉的英國著重對代數及代數在幾何方面的套用研究這樣的背景下。矩陣理論對線性變換的研究引進了向量的代數定義，而這是張量概念的先導。
另一方面,格奧爾格·弗雷德里希·波恩哈德·黎曼( Georg Friedrich Bernhard Riemann)提出的n維流形的概念，這在客觀上提出了深入研究代數形式的課題。黎曼的幾何思想在拓展幾何學的同時,提高了代數在表達幾何對象方面的抽象程度。黎曼之後，在克里斯托弗、里奇和列維-契維塔等人的努力下,形成了張量分析這樣的數學方法，黎曼幾何學也因此而建立起來了。
2.張量的定義、性質與套用價值
從代數角度講， 它是向量的推廣。我們知道，向量可以看成一維的“表格”（即分量按照順序排成一排），矩陣是二維的“表格”（分量按照縱橫位置排列）， 那么n階張量就是所謂的n維的“表格”。張量的嚴格定義是利用線性映射來描述的。與矢量相類似，定義由若干坐標系改變時滿足一定坐標轉化關係的有序數組成的集合為張量。
標量可以看作是0階張量，矢量可以看作1階張量。張量中有許多特殊的形式， 比如對稱張量、反對稱張量等等。
有時候，人們直接在一個坐標系下，由若干個數（稱為分量）來表示張量，而在不同坐標系下的分量之間應滿足一定的變換規則（參見協變規律，反變規律），如矩陣、多變數線性形式等都滿足這些規律。一些物理量如彈性體的應力、應變以及運動物體的能量、動量等都需用張量來表示。在微分幾何的發展中，C.F.高斯、B.黎曼、E.B.克里斯托費爾等人在19世紀就導入了張量的概念，隨後由G.里奇及其學生T.列維齊維塔發展成張量分析，A.愛因斯坦在其廣義相對論中廣泛地利用了張量。
黎曼幾何作為非歐幾何的一種,它與羅巴切夫斯基幾何相比，有著實質性的不同。羅氏幾何主要工作是建立了一整套區別於歐幾里得的《幾何原本》的邏輯體系； 而黎曼幾何的核心問題是以微分幾何為基礎,建立曲線坐標系中的微分方法。羅氏幾何是第一個被提出的非歐幾何學，它的基本觀點是： 第一,第五公設不能被證明; 第二，可以在新的公理體系中展開一連串推理,得到一系列在邏輯上無矛盾的新的定理，形成新的理論。羅氏幾何學的公理系統區別於歐式幾何學之處,僅僅是把歐式幾何平行公理改為: 從直線外一點，至少可以做兩條直線和這條直線平行。黎曼幾何與羅氏幾何的平行公理相反： 過直線外一點,不能做直線和已知直線平行。也就是說，黎曼幾何規定: 在同一平面內任何兩條直線都有公共點,黎曼幾何學不承認存在平行線。很自然就有另一條公設： 直線可以延長至任意長度，但長度是有限的,這可以類比為一個球面。黎曼幾何是通過微分幾何的途徑建立起來的，因此與羅氏幾何根本不同。
黎曼幾何學的公理體系引進了一種彎曲的幾何空間(它可以通過拉梅引進的曲線坐標系描述),黎曼在構想這種幾何學的時候，就想設法建立起相應的代數結構。這個目標黎曼本人沒有實現,但沿著他開闢的道路，克里斯托夫和里奇完成了新幾何學的構建。換句話說,張量分析構成了黎曼幾何學的核心內容。這表現在若干方面: 1.黎曼空間中的曲率是一個張量，其有關運算需採用絕對微分法； 2. 黎曼空間的度量以度量張量表達; 3. 黎曼空間的平行定義為標積保持不變(即與曲線的夾角保持不變),依賴克里斯托夫符號； 4. 黎曼空間的直線(短程線)方程的建立依賴協變微分。正因為有了張量分析這個工具，黎曼幾何才獲得了類似於微積分一樣的計算功能,從而擺脫了停留在邏輯構造層面上的束縛，從根本上與微分幾何實現了傳承,並實現了微分幾何從直線坐標繫到曲線坐標系的進步，使得幾何學與代數學更緊密地聯繫起來。
