基本介紹
介紹
記號
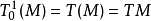


套用


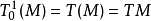



是物理學中場的一種。假如一個空間中的每一點的屬性都可以以一個張量來代表的話,那么這個場就是一個張量場。最常見的張量場有廣義相對論的應力能張量場(Stress...
張量(tensor)理論是數學的一個分支學科,在力學中有重要套用。張量這一術語起源於力學,它最初是用來表示彈性介質中各點應力狀態的,後來張量理論發展成為力學和物理學...
張量分析是微分幾何中研究張量場的微分運算的一個分支。張量分析是用共變微分表示各種幾何量和微分運算元性質的運算方法,可以看作是微分流形上的“微分法”,是研究流...
應力一能量張量(stress-energy tensor)由映射確定的一個特殊張量.若f:M->N是光滑映射,M和N的黎曼度量張量分別為g和h,f的能量密度為。(f),則"Sf=e }.f ...
曲率張量(curvature tensor)由聯絡確定的一個重要張量。曲率張量是一個重要的數學量。在眾人所關注的廣義相對論中起到了重要的作用。沒有曲率張量,就不可能建立起...
《張量分析》以線性仿射空間和多重線性代數為基礎,從代數結構、拓撲結構、微分結構三個角度系統完整地闡述了張量分析。全書共分為5章:線性空間;矢量代數和矢量分析;...
《張量分析》是一本系統闡述張量分析的專著,又是易於教學的教材。全書共分6章。內容包括:矢量與張量的基本概念與代數運算,二階張量,張量函式及其導數,曲線坐標張量...
《張量和連續介質力學》是2012年12月冶金工業出版社出版的圖書,作者是黃寶宗。...... 《張量和連續介質力學》是2012年12月冶金工業出版社出版的圖書,作者是黃寶宗...
《張量分析簡明教程》是2010年同濟大學出版社出版的圖書,作者是張若京。...... 本書介紹張量分析的基本內容,包括空間曲線坐標系、張量的基本概念和代數運算、張量場論...
《彈性力學與張量分析》是2003年高等教育出版社圖書發行部(蘭色暢想)出版的圖書,作者是郭日修。本書供高等學校船舶與海洋工程等工程專業作研究生教材用,也可供高等...
《張量分析及其在連續介質力學中的套用》是哈爾濱工程大學出版社2005年出版的數學工具書,作者張耀良。...
《張量分析教程》是2004年同濟大學出版社出版的一本圖書,作者是張若京,主要介紹張量分析的基本內容。...
《張量分析(第2版)(北京高等教育精品教材)》是2014年8月27日出版的圖書,作者黃克智等。...
中文名 關於D維伸縮子-反對稱張量場-引力系統的黑膜解的研究 學位授予單位 中國科學院理論物理研究所 學科專業 理論物理 作者 周彬...
2.1.3 物理向量場與切空間 2.1.4 定律協變性背景下的流形張量場. 2.1.5 流形上協變微分與聯絡 2.1.6 張量不變數的物理意義 2.2 流形上的向量場 ...
李導數(Lie derivative)是一種對流形 M 上的張量場,向量場或函式沿著某個向量場的求導運算,以索甫斯·李命名。所有李導數組成的向量空間對應於如下的李括弧...
