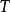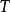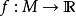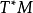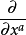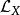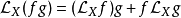基本介紹
- 中文名:李導數
- 外文名:Lie derivative
- 領域:數理科學
- 人物:索甫斯·李
簡介,定義,性質,和外導數的關係、微分形式的李導數,張量場的李導數,
簡介
定義





然後定義向量場Y的李導數等於X和Y的李導數,也就是,

根據上面任選的一個定義,其他的定義可被證明為其等價形式。 例如,可以證明,對於一個可微函式f, 並且
並且


我們用在1-形式 上的李導數的定義來結叢本節:
上的李導數的定義來結叢本節: .
.


性質
類似的,它是 上的一個導數,其中
上的一個導數,其中 是M上的向量場的集合:
是M上的向量場的集合:



也可寫為等價形式

其中張量積符號 用於強調函式和向量場的積在整個流形上取。另外的性質和李括弧的一致。所以,例如,作為向量場的導數,
用於強調函式和向量場的積在整個流形上取。另外的性質和李括弧的一致。所以,例如,作為向量場的導數,

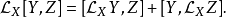
和外導數的關係、微分形式的李導數
令M為一個流形,X為M上一個向量場。令 為一k+1-形式。X和ω的內積為
為一k+1-形式。X和ω的內積為


注意, 是
是 -反導數。也就是,是R-線性的,並且
-反導數。也就是,是R-線性的,並且 。
。



對於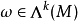 和另一個微分形式η成立。另外,對於一個函式
和另一個微分形式η成立。另外,對於一個函式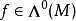 ,那是一個實或復值 的M上的函式,有
,那是一個實或復值 的M上的函式,有
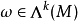
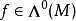

外導數和李導數的關係可以總結為以下這些。對於一般函式f,李導數就是外導數和向量場的內積:


當ω為1-形式,上述恆等式經常寫作

導數的乘積是可分配的

張量場的李導數
在微分幾何中,如果我們有一個 階可微張量場(我們可以把它當作餘切叢
階可微張量場(我們可以把它當作餘切叢 的光滑截面
的光滑截面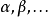 和切叢
和切叢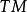 的截面
的截面 的線性映射
的線性映射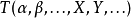 ),使得對於任何函式
),使得對於任何函式 有
有 而且如果進一步有一個可微向量場(也就是切叢的一個光滑截面)
而且如果進一步有一個可微向量場(也就是切叢的一個光滑截面) ,則線性映射
,則線性映射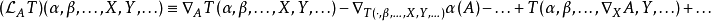 獨立於聯絡∇;只要它是無撓率的,事實上,這個映射是一個張量。這個張量稱為
獨立於聯絡∇;只要它是無撓率的,事實上,這個映射是一個張量。這個張量稱為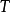 關於
關於 的李導數。
的李導數。


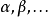
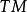

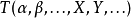



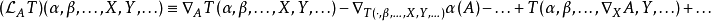
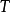

換句話說,如果你有一個張量場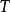 和一個由向量場
和一個由向量場 給出的微分同胚的無窮小生成元,則
給出的微分同胚的無窮小生成元,則 就是
就是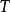 在這個無窮小微分同胚下的無窮小變化。
在這個無窮小微分同胚下的無窮小變化。