基本介紹
- 中文名:切空間
- 外文名:tangent space
- 領域:數學
- 意義:切向量組成的線性空間
- 概念:歐式空間的推廣
- 對象:微分流形
線性空間
切向量
切空間詳細定義
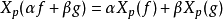

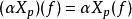
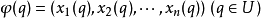
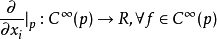
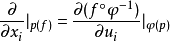
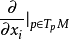
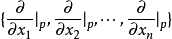
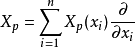
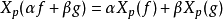

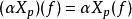
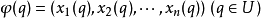
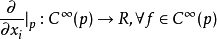
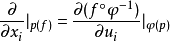
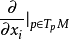
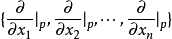
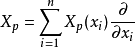
切空間是在某一點所有的切向量組成的線性空間。切空間是微分流形在一點處所聯繫的向量空間,歐氏空間中光滑曲線的切線、光滑曲面的切平面的推廣。切向量是切線的...
人們從直觀上觀察到空間三維(或三度)和一維時間,相對論稱為“四維時空”。對於超四維空間人們一直是處於支持和反對的態度。有人認為巨觀世界空間是三維的;微觀世界...
切層是代數簇上的點的切空間構成的層。更精確地說,對於代數簇 X,切層就是 X 上一次微分所構成的層的對偶層。...
切纖維叢(tangent fiber bundle)是E流形上的每一點切空間的並所組成的纖維叢。...... 切纖維叢(tangent fiber bundle)是E流形上的每一點切空間的並所組成的...
餘切向量是切向量的對偶概念。 流形M在點P處的切向量全體構成切空間,切空間的 對偶空間就是餘切空間。 餘切向量就是餘切空間中的向量。 粗略的說,餘切向量就是...
黎曼流形(Riemannian manifold)是一個微分流形,其中每點 p 的切空間都定義了點積,而且其數值隨 p 平滑地改變。它容許我們定義弧線長度,角度,面積,體積,曲率,...
是取定的,將指數映射 exp 限制在切空間 上得到 稱為黎曼流形 M 在點 p 的指數映射。如果不假定 M 是完備的,則指數映射 exp 在切叢 TM 中圍繞零截面的一...
微分幾何中,流形的餘切叢是流形每點的切空間組成的向量叢。本身作為一個流形的餘切叢總是可定向的。...
微分幾何中,第二基本形式(second fundamental form)是三維歐幾里得空間中一個光滑曲面的切叢上一個二次形式,通常記作 II。與第一基本形式一起,他們可定義曲面的...
微分流形(differentiable manifold),也稱為光滑流形(smooth manifold),是拓撲學和幾何學中一類重要的空間,是帶有微分結構的拓撲流形。 微分流形是微分幾何與微分...
是Riemann對稱空間,又 對應Cartan分解為 為 的切空間,S是M的子流形,S在 處切空間為 於是有1) 若S為M的全測地子流形,則有滿足...
幾何概念,它們是辛子流形(可以是任何偶數維)和拉格朗日子流形(一半維度),其中辛流形要導出該子流形上的一個辛形式,而辛流形限制到拉格朗日子流形的切空間上時...
