切纖維叢

切纖維叢（tangent fiber bundle）是E流形上的每一點切空間的並所組成的纖維叢。

基本介紹

• 中文名：切纖維叢
• 外文名：tangent fiber bundle
• 適用範圍：數理科學

簡介

切纖維叢是E流形上的每一點切空間的並所組成的纖維叢。

設 X 是有圖冊的E流形，令

，關於，令

其中 是 在 之下的代表，則容易驗證，含的最大圖冊，構成 T(X)的一個圖冊，在此圖冊之下，T(X)成為模型在 E×E內的 流形，成為 E 流形X的切叢。

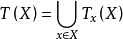
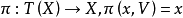
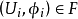
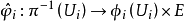
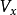
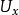
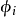
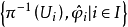
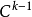
另一方面，叢纖維叢的角度，把一切與T(X)有關的對象集中於一起，可以寫為(T(X),X,π,E,GL(E))，它是一個纖維叢，以T(X) 為全空間，X為底空間，E為典型纖維以及GL(E) 為結構群。

性質

若 v 是切纖維叢T(X)的一個截面，即映射

使得，則 v 稱為X上的向量場。

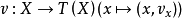
纖維叢

纖維叢的理論，是1946年由美國的斯丁路特、美籍華人陳省身、法國的艾勒斯曼共同提出的。

數學上，特別是在拓撲學中，一個纖維叢(fiber/fibre bundle)是一個局部看來像兩個空間的直積（特指笛卡爾積）的空間，但是整體可以有與直積空間不同的拓撲結構。