坐標叢在嚴格等價之下的一個等價類稱為一個纖維叢。由於每一個坐標叢都惟一地決定了一個纖維叢,故通常當得到一個坐標叢時,就認為得到了一個纖維叢,且簡記為(E,B,π,F,G)。
基本介紹
- 中文名:坐標叢
- 適用範圍:數理科學
簡介,表示方法,性質,
簡介
設空間 E 稱為全空間,空間 B 稱為底空間,連續映射π:E→B 稱為投影,空間 F 稱為典型纖維,G 位作用在F上的有效拓撲變換群,稱為結構群, 為B的開覆蓋,且對每個 Vj 有同胚
為B的開覆蓋,且對每個 Vj 有同胚



1、 ,對任意
,對任意 和任意 y∈F;
和任意 y∈F;


2、令 為
為 ,則對任意
,則對任意 ,同胚
,同胚 ,屬於 G;
,屬於 G;




3、對任意 ,由
,由 定義的映射
定義的映射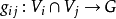 連續,
連續, 稱為轉移函式族,
稱為轉移函式族,



表示方法
坐標叢記為
性質
若兩個具有相同的全空間、底空間、投影、典型纖維和結構群的坐標叢的兩個轉移函式族合併起來仍滿足條件1,2和3,即仍成為一個轉移函式族,則稱這兩個坐標叢嚴格等價。
坐標叢在嚴格等價之下的一個等價類稱為一個纖維叢。
由於每一個坐標叢都惟一地決定了一個纖維叢,故通常當得到一個坐標叢時,就認為得到了一個纖維叢,且簡記為(E,B,π,F,G),當G無需指明時也簡記為(E,B,π,F),當F,G和π無需指明時也說E是B上的一個纖維叢。例如,若M是n維微分流形,其切叢T(M)在自然投影π之下是M上的一個纖維叢,實際上是以T(M)為全空間,M為底空間,π為投影,Rn為典型纖維,一般線性群 GL(n,R)為結構群的纖維叢。


