Ck類可微纖維叢

C^k類可微纖維叢（differentiable fiber bundle of class Ck）是轉移函式是C^k可微的纖維叢。

基本介紹

• 中文名：Ck類可微纖維叢
• 外文名：differentiable fiber bundle of class Ck
• 適用範圍：數理科學

簡介

C^k類可微纖維叢是轉移函式是C^k可微的纖維叢。

若坐標叢(E,B,π,F,G)中E,B,F均為C^k微分流形，G為一個李群，且圖冊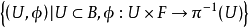

中的U是B的微分結構的定義域，轉移函式g_ij:U_i∩U_j→G是C_k可微的，則(E,B,π,F,G)稱為C^k類可微纖維叢。

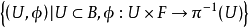
實例

作為例子，n維C^k微分流形M的切叢T(M)使(T(M),M,π,Rⁿ,GL(n,R))成為一個C^k-1類可微纖維叢，亦稱C^k-1類微分切叢。

纖維叢

纖維叢的理論，是1946年由美國的斯丁路特、美籍華人陳省身、法國的艾勒斯曼共同提出的。數學上，特別是在拓撲學中，一個纖維叢(fiber/fibre bundle)是一個局部看來像兩個空間的直積（特指笛卡爾積）的空間，但是整體可以有與直積空間不同的拓撲結構。

纖維叢擴展了矢量叢，矢量叢的重要實例就是流形的切叢和餘切叢。他們在微分拓撲和微分幾何領域有著重要的作用，也是規範場論的基本概念。