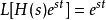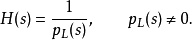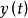基本介紹
- 中文名:轉移函式
- 外文名:transfer function
- 對應:描述其運動規律的微分方程
- 類型:數學函式
- 套用領域:自動控制理論
基本釋義,推導,性質,套用,
基本釋義
把具有線性特性的對象的輸入與輸出間的關係,用一個函式(輸出波形的拉普拉斯變換與輸入波形的拉普拉斯變換之比)來表示的,稱為轉移函式。原是控制工程學的用語,在生理學上往往用來表述心臟、呼吸器官、瞳孔等的特性。
系統的轉移函式與描述其運動規律的微分方程是對應的。可根據組成系統各單元的轉移函式和它們之間的聯結關係導出整體系統的轉移函式,並用它分析系統的動態特性、穩定性,或根據給定要求綜合控制系統,設計滿意的控制器。以轉移函式為工具分析和綜合控制系統的方法稱為頻域法。它不但是經典控制理論的基礎,而且在以時域方法為基礎的現代控制理論發展過程中,也不斷發展形成了多變數頻域控制理論,成為研究多變數控制系統的有力工具。轉移函式中的復變數s在實部為零、虛部為角頻率時就是頻率回響。
轉移函式也是《積分變換》里的概念。對復參數s,函式f(t)*e^(-st)在(-∞,+∞)的積分,稱為函式f(t)的(雙邊)拉普拉斯變換,簡稱拉氏變換(如果是在[0,+∞)內積分,則稱為單邊拉普拉斯變換,記作F(s),這是個複變函數。
設一個系統的輸入函式為x(t),輸出函式為y(t),則y(t)的拉氏變換Y(s)與x(t)的拉氏變換X(s)的商:W(s)=Y(s)/X(s)稱為這個系統的轉移函式。
轉移函式的概念在自動控制理論里有重要套用。
推導
或者在離散時間系統中,套用Z變換,轉移函式可以類似地表示成這常常被稱為脈衝轉移函式。



從微分方程直接推導
考慮一個常係數線性微分方程
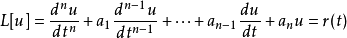

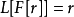
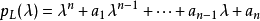
在輸入函式r的形式也為 的時候,非齊次的情形也可以很容易的解決。在那種情況下,通過代入
的時候,非齊次的情形也可以很容易的解決。在那種情況下,通過代入 就可以發現
就可以發現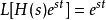 若且唯若
若且唯若