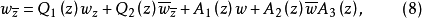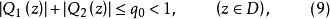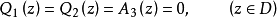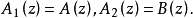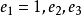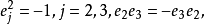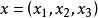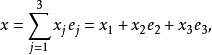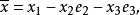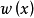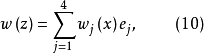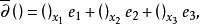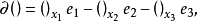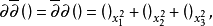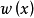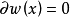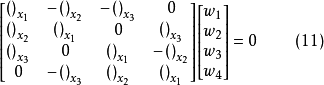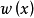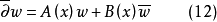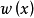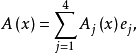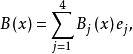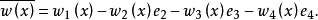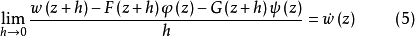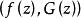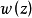廣義解析函式

廣義解析函式(generalized analytic function)是解析函式的推廣，指標準化的一階橢圓型方程組在平面區域D內的連續解。韋夸(И.И.Векуа)和伯斯(L.Bers)各自獨立地建立了系統的廣義解析函式理論。20世紀50年代，亞音速、超音速飛機的研製，推進了廣義解析函式的發展。

基本介紹

• 中文名：廣義解析函式
• 外文名：generalized analytic function
• 所屬領域：複變函數論
• 相關概念：解析函式、第一類準解析函式等

定義

廣義解析函式(generalized analytic function)是解析函式的推廣。指標準化的一階橢圓型方程組

在平面區域D內的連續解，以上方程組還可寫成復形式的方程

其中

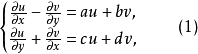
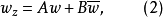
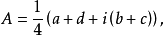
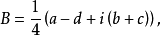
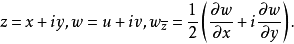
相關性質概念

韋夸(И.И.Векуа)和伯斯(L.Bers)各自獨立地建立了系統的廣義解析函式理論。20世紀50年代，亞音速、超音速飛機的研製，推進了廣義解析函式的發展，伯斯用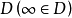內兩個連續可微的函式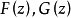分別代替複數表示中的1，i，並要求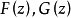滿足條件

而D內任一連續可微函式均可表示成

這裡φ(z)，ψ(z)都是D內實值函式，如果對D內的任一點z，極限

存在，則稱按在點z存在微商，並稱為D內的第一類準解析函式，是D內第一類準解析函式的充分必要條件是：在D內滿足複方程(2)，其中

還可以證明：在D內滿足複方程

並稱為D內的第二類準解析函式，這兩類準解析函式有著不同的性質，對於非常數的第二類準解析函式，保持區域定理是成立的，而對於第一類準解析函式，保持區域定理不一定成立。設是區域D內廣義解析函式或第一類準解析函式，則必存在D內解析函式與上的連續函式，使得

這個定理稱為相似原理。有了這個原理，使得關於解析函式的許多性質，可轉移到廣義解析函式上來，如積分和級數理論、孤立奇點的分類、惟一開拓性、函式序列的凝聚原理及龍格逼近定理等。類似於解析函式，對於複方程(2)，也有各種邊值問題的可解性結果等，如黎曼邊值問題和黎曼-希爾伯特邊值問題，這些邊值問題在力學、物理學中有重要套用。

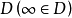
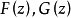
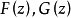
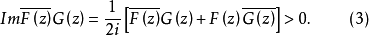
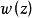
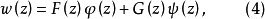
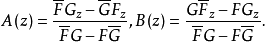
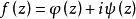
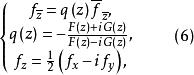
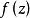
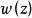
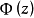
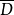
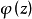
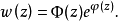
方程組(1)和複方程(2)可推廣到一階線性一致橢圓型方程組和一致橢圓型複方程

其一致橢圓型條件為

這裡q₀是非負常數，特別地，當

時，(8)就是複方程(2)，其中

對於多個自變數的情況，在克利福德代數的基礎上，建立了相應於單複變函數的一些理論，以三個實自變數的情況為例，用，表示克利福德代數的基，其中設D是三維歐氏空間R³中的區域，D內的點可寫成

而又D內的函式可表為

這裡用e₄表示e₂e₃，定義運算

顯然區域D內的正則函式是指滿足方程組，即

的連續函式，又廣義正則函式是指D內滿足方程組

的連續函式，其中