馬爾可夫轉移函式(Markov transition func-lion)由馬爾可夫過程的轉移函式引申出來的概念。
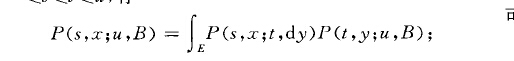
馬爾可夫轉移函式(Markov transition func-lion)由馬爾可夫過程的轉移函式引申出來的概念。
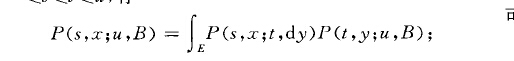
馬爾可夫轉移函式(Markov transition func-lion)由馬爾可夫過程的轉移函式引申出來的概念。...
如果Xn + 1對於過去狀態的條件機率分布僅是Xn的一個函式,則P(Xn+1=x∣X0...使用馬爾科夫模型進行人力資源供給預測的關鍵是確定出人員轉移率矩陣表,而在實際...
馬爾可夫預測法主要用於市場占有率的預測和銷售期望利潤的預測。就是一種預測事件發生的機率的方法。馬爾科夫預測講述了有關隨機變數、 隨機函式與隨機過程。...
馬爾可夫決策過程值函式 參見:強化學習MDP的每組軌跡都對應一個(折現)回報。由於MDP的策略和狀態轉移都是條件機率,因此在考慮模型的隨機性後,軌跡的折現回報可以由其...
由於馬爾可夫過程的狀態空間是可數集,在連續時間下其樣本軌道幾乎必然(a.s.)是右連續的片段函式,因此馬爾可夫過程可以表示為跳躍過程(jump process)並與馬爾可夫鏈...
安德雷·安德耶維齊·馬爾可夫АндрейАндреевичМарков(...本人在數學的若干領域也作出了開拓性的貢獻,特別是在數論、機率論和函式逼近論...
因此,運算元族{Tt}t∈R+構成運算元半群,這就是馬爾可夫(轉移)半群。由於這個半群總可完全惟一地決定過程的轉移函式,考慮馬爾可夫過程相應的運算元半群是很有好處的。...
馬爾可夫的主要貢獻在機率論、數論、函式逼近論和微分方程等方面。在機率論方面,他深入研究並發展了切比雪夫的矩方法,使中心極限定理的證明成為可能。他還推廣了大數...
模型是一個雙重隨機過程---具有一定狀態數的隱馬爾可夫鏈和顯示隨機函式集。自...在簡單的馬爾可夫模型(如馬爾可夫鏈),所述狀態是直接可見的觀察者,因此狀態轉移...
所以,隱馬爾可夫模型是一個雙重隨機過程---具有一定狀態數的隱馬爾可夫鏈和顯示隨機函式集。一般的,可以用λ=(A,B,π)三元組來簡潔的表示一個隱馬爾可夫模型。隱...
和 G均蛻化為確定性函式時,可以把事件的發生看成由某種外生的機制來決定的,則就又回到邏輯層的有限自動機模型,有人將它稱為廣義半馬爾可夫格式.這也說明了離散...
3·3 強馬爾可夫性第四章 馬爾可夫鏈中的幾個問題4·1 0-1律4·2 常返性與過份函式4·3 積分型隨機泛函的分布4·4 嵌入問題第五章 生滅過程的基本理論...
《馬爾可夫決策過程理論與套用》是2015年科學出版社出版的圖書,作者是劉克、曹平...發生轉移的規律等等.當然,決策的目的是要最佳化決策者關心的目標函式,使得目標函式...
62.隨機變數的馬爾可夫-布倫斯鏈∥235第七章 複雜鏈∥23763.馬爾可夫的情形∥23764.雙聯結鏈的一般情形∥24165.鏈C(2)n的特徵函式∥244...
(3)蒙特卡洛積分:任一函式f(x)的期望估計為: 。 [1] MCMC中採樣算法如圖2所示。圖2 馬爾科夫鏈蒙特卡洛方法方法 編輯 在採用MCMC方法時,馬爾科夫鏈轉移核的...
純間斷馬爾可夫過程(purely discontinuousM arkov process)亦稱馬爾可夫跳躍過程一類...(t,x>}0是跳躍強度函式,Q(t,x,戶是條件分布函式.因而有P (t,x;t+at,...
62.隨機變數的馬爾可夫—布倫斯鏈 第七章複雜鏈 63.馬爾可夫的情形 64.雙聯結鏈的一般情形 65.鏈Cn(2)的特徵函式 66.多聯結鏈 67.無限複雜鏈 68...
二、三,以及更多步的轉移機率可以導自一步轉移機率和馬爾可夫性質:...一個平穩分布是一個對應於特徵值為1的條件分布函式的特徵方程。...
費勒過程(Feller process)是一類馬爾可夫過程,指其對應的轉移運算元把連續函式映為連續函式的馬爾可夫過程.設E為距離空間,省為E上開集產生的。...
預解運算元族(resolvent operators)亦稱預解式,是研究馬爾可夫半群和對應的無窮小運算元的重要工具。和無窮小運算元A一樣,此處仍只考慮馬爾可夫過程的轉移函式。對每一複數...
