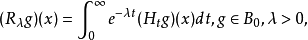基本介紹
- 中文名:預解運算元族
- 外文名:resolvent operators
- 別名:預解式
- 套用:馬爾可夫半群
- 工具:馬爾可夫過程的轉移函式
- 學科:數學
定義,推導過程,
定義
預解運算元族(resolvent operators)亦稱預解式,是研究馬爾可夫半群和對應的無窮小運算元的重要工具。和無窮小運算元A一樣,此處仍只考慮馬爾可夫過程的轉移函式。對每一複數λ(Reλ>0),定義運算元Rλ:

對每個複數λ(Re λ>0),Rλ是線性有界運算元。雖然預解運算元族不一定能唯一地決定半群{Tt}(因為對任意x,Γ∈E由Rλ只能對幾乎所有t>0求出P(t,x,Γ),而不是對所有t>0),但在研究Tt與它的無窮小運算元A的關係時,Rλ是一個重要工具。
推導過程
設P(t,x,B)是時齊馬氏過程X={Xt,t≥0}的時齊轉移分布,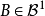 ,記
,記
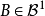
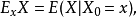



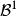

對每一t≥0,記

如果gn,g∈B並且當 時,有
時,有


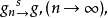

令B0={g:g∈B,且存在極限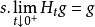 },定義
},定義