基本介紹
- 中文名:無窮小運算元
- 外文名:infinitesimal operator
- 所屬學科:數學
- 所屬問題:隨機過程理論的重要概念
- 別稱:無窮小生成元
基本介紹
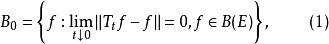
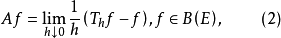
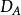
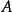
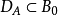
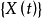
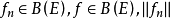
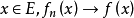
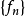
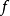
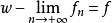
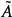
馬爾可夫過程的無窮小運算元
定義
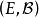
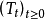
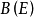
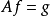
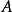
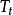
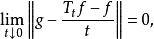
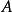
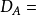
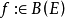
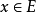
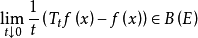
無窮小運算元性質
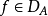
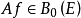
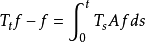
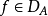
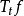
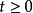
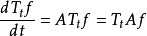
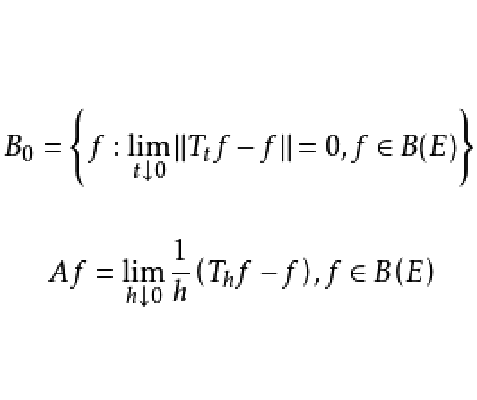
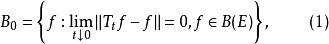
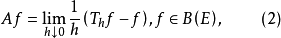
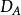
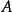
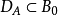
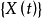
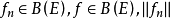
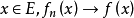
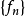
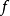
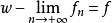
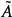
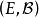
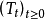
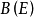
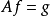
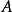
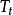
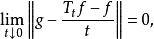
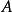
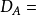
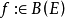
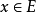
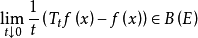
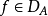
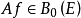
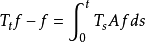
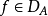
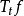
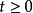
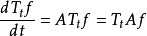
無窮小運算元(infinitesimal operator)亦稱無窮小生成元,是隨機過程理論的重要概念,它可對任意巴拿赫空間上的任一運算元半群來定義,是由運算元半群決定的閉線性運算元。...
主要代表作有《無窮維線性反應擴散過程的極限狀態》,《一類反應擴散過程的無窮小運算元在Banach和Hilbert空間的有界性》及《具有Poisson大周期的股票價格過程及其期權定價...
A3.3.3 投影運算元 附錄A4 李群和李代數 A4.1 李群的概念 A4.1.1 連續群的概念 A4.1.2 李群的概念 A4.1.3 李群的例子 A4.2 李群的無窮小運算元、...
2.3無窮小運算元 2.4 Lie代數 2.5 Casimir不變運算元 2.6 Casimir運算元的本徵值 參考文獻 第3章動力學對稱性 3.1二維諧振子動力學對稱性 3.2四維諧振子...
7.1 李群與無窮小運算元 7.2 李代數 7.3 李群與李代數的表示 7.4 李群的一些整體性質 7.5 Wigner—Eckart定理與張量運算元 7.6 李群的套用實例 習題 第8章 ...
5.1 右連續Feller過程的廣無窮小運算元 5.2 一維連續Feller過程 5.3 樣本函式的連續性條件 5.4 補充與習題 參考文獻 第6章 間斷型馬爾可夫過程 6.1 轉移機率的...
};-p';;(0)作元素的方陣(qi、)稱為轉移機率矩陣(p;;(t))的Q矩陣.它是相應的轉移矩陣(或者說,馬爾可夫鏈)的轉移強度矩陣(又稱密度矩陣或無窮小運算元)....
投影運算元附錄A4 李群和李代數 A4.1 李群的概念 A4.1.1 連續群的概念 A4.1.2 李群的概念 A4.1.3 李群的例子 A4.2 李群的無窮小運算元、李代數 A4.2.1 李群...
60年代,利用自己建立的“降運算元多項式”在國際上首先證明了著名蘇聯數學家Gelfand的U(n)群無窮小運算元矩陣元公式,該公式在核物理和量子化學中被廣泛套用;拓樸性是70...
60年代,利用自己建立的“降運算元多項式”在國際上首先證明了著名蘇聯數學家Gelfand的U(n)群無窮小運算元矩陣元公式,該公式在核物理和量子化學中被廣泛套用;拓樸性是70...
究其原因主要是由於此時過程的時間參數無全序關係,我們在單參數馬氏過程研究中使用的首達時、無窮小運算元等的方法已無法借鑑,需要引進新的概念和方法,但目前在此...
