單位張量(unit tensor)合成代數的單位元。
張量理論是數學的一個分支學科,在力學中有重要套用。張量這一術語起源於力學,它最初是用來表示彈性介質中各點應力狀態的,後來張量理論發展成為物理學的一個有利的數學工具。
基本介紹
- 中文名:單位張量
- 外文名:unit tensor
- 適用範圍:數理科學
定義介紹

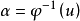
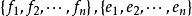
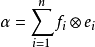
合成代數

張量
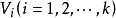
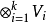
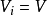
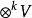
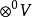


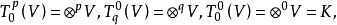


單位張量(unit tensor)合成代數的單位元。
張量理論是數學的一個分支學科,在力學中有重要套用。張量這一術語起源於力學,它最初是用來表示彈性介質中各點應力狀態的,後來張量理論發展成為物理學的一個有利的數學工具。

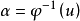
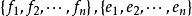
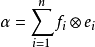

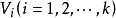
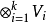
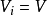
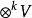
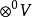


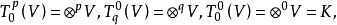

單位張量(unit tensor)合成代數的單位元。張量理論是數學的一個分支學科,在力學中有重要套用。張量這一術語起源於力學,它最初是用來表示彈性介質中各點應力狀態的,...
電磁張量(electromagnetic tensor)或電磁場張量(electromagnetic field tensor)(有時也稱作場強張量(field strength tensor)、法拉第張量(Faraday tensor)或麥克斯韋雙矢量...
在多重線性代數裡,並矢張量(dyadic tensor)是一個以特別標記法寫出的二階張量,是由成對的向量並置形成的。針對這特別標記法,有一套專門計算這種表達式,類似於...
在電磁學裡,麥克斯韋應力張量(Maxwell stress tensor)是描述電磁場帶有之應力的二階張量。麥克斯韋應力張量可以表現出電場力、磁場力和機械動量之間的相互作用。...
《張量分析及在力學中的套用(第2版)》系統闡述了張量分析及其在力學中的套用。全書共分9章,第1,2章介紹張量的基礎知識,第3~6章介紹張量代數、張量分析和黎曼...
曲率張量(curvature tensor)由聯絡確定的一個重要張量。曲率張量是一個重要的數學量。在眾人所關注的廣義相對論中起到了重要的作用。沒有曲率張量,就不可能建立起...
在微分幾何中,類似度量張量,里奇張量也是一個在黎曼流形每點的切空間上的對稱雙線性形式。以格雷戈里奧·里奇-庫爾巴斯托羅(Gregorio Ricci-Curbastro)為名的里奇...
物理學中,電磁應力-能量張量是指由電磁場貢獻於應力-能量張量(又稱能量-動量張量)的部份。...
物理量單位通過物理定律及其方程建立相互間的關係。它們中有的有方向,有的無方向;有的有量綱(見量綱分析)、單位 ,有的無量綱、單位;有的描述狀態,有的描述過程;...
‘與八E的反張量積,記為八E"②八E.它是具有單位元1②1,且由1②1,E *②1與1②E生成的非交換的結合代數.由定義,d W, E八rE*⑨八“E, WZ E八'E ...
協變張量(covariant tensor)是指所有指標都是協變的張量。既有協變又有逆變的張量為混合張量。...
2018年3月6日,巴彥淖爾市人大常委會任命張量為巴彥淖爾市安全生產監督管理局局長。1 ...
《張量分析(第2版)(北京高等教育精品教材)》是2014年8月27日出版的圖書,作者黃克智等。...
為單位張量,標架 是一個典型的單位正交曲線標架; 是剛體的密度。轉動慣量張量的力矩方程設剛體A所受到的繞其質心C的合力矩矢量為 ,剛體A在慣性系下的角速度...
