協變張量(covariant tensor)是指所有指標都是協變的張量。既有協變又有逆變的張量為混合張量。
基本介紹
- 中文名:協變張量
- 外文名:covariant tensor
- 所屬學科:數學(張量分析)
- 簡介:所有指標都是協變的張量
- 相關概念:混合張量,協變矢量等
(協變)張量的定義
坐標系的變換關係




 圖1(a)標架變換
圖1(a)標架變換 圖1(b)標架變換
圖1(b)標架變換

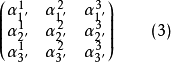



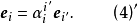
標量(純量Scalar)
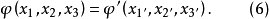
協變矢量


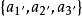



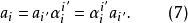




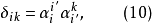
推廣到協變張量
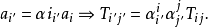
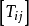

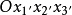
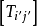
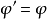
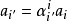

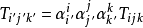



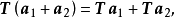


向量空間的張量代數

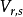

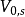
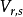

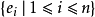

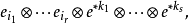

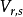





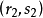

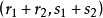

協變張量(covariant tensor)是指所有指標都是協變的張量。既有協變又有逆變的張量為混合張量。




 圖1(a)標架變換
圖1(a)標架變換 圖1(b)標架變換
圖1(b)標架變換

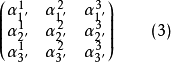



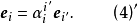
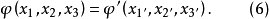


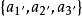



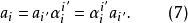




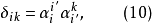
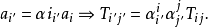
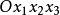

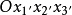
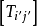
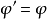
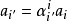

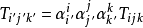



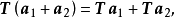




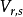

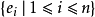

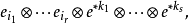

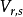





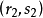

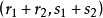
由於變換方式的不同,張量分成協變張量 (Covariant Tensor,指標在下者)、逆變張量 (Contravariant Tensor,指標在上者)、 混合張量 (指標在上和指標在下兩者都有) ...
協變張量(covariant tensor)是指所有指標都是協變的張量。既有協變又有逆變的張量為混合張量。...
協變振幅的張量分析論文作者是朱界傑,導師是阮圖南教授...... 協變振幅的張量分析論文作者是朱界傑,導師是阮圖南教授 副題名外文題名論文作者朱界傑著導師...
在評估過所有分量後,可以得到一個二階、反對稱、協變張量 :場強張量在量子電動力學與量子場論中的角色 編輯 在量子電動力學中的拉格朗日量是從相對論建立的經典...
有兩個(或更多)張量積的分量的一般公式。例如,如果U和V是秩分別為n和m的兩個協變張量,則它們的張量積的分量給出為:所以兩個張量的張量積的分量是每個張量的...
,度量張量為二階張量一般表示為 ,也可以用矩陣表示,記作為G或g。而 記號傳統地表示度量張量的協變分量(亦為“矩陣元素”)。度量...
物質場的能量密度、動量密度、動量流密度統一組合成一個二階的協變張量,稱為能動張量,用Tab表示。能動張量性質 編輯 對稱,Tab=Tab。 能動張量的協變散度為0,...
張量分析是微分幾何中研究張量場的微分運算的一個分支。張量分析是用共變微分表示各種幾何量和微分運算元性質的運算方法,可以看作是微分流形上的“微分法”,是研究流...
所以,並矢張量是一個二階協變張量。反過來說,按照這定義推廣,任意二階協變張量都是並矢張量:。並矢張量並矢張量運算 編輯 套用點積,並矢張量 可以與向量 綜合...
它涉及到協變導數:給定流形某點的任一坐標表示,上述恆等式可以用黎曼曲率張量的分量形式表示為:第一(代數)比安基恆等式:或等價地寫為 第二(微分)比安基恆等式:...
前面所說的xμ、jμ、Aμ和這裡的微分算符都是逆變矢量,而微分算符則為共變矢量。式 (8)中每一項都代表一個三階的逆變張量,故該式是協變的。 這裡,對於...
內容包括:矢量與張量的基本概念與代數運算,二階張量,張量函式及其導數,曲線坐標...1.2.2.2 協變基矢量1.2.2.3 逆變基矢量1.2.2.4 由協變基矢量求逆變...
9.3Matlab的張量運算 9.4Mathematica的張量運算 習題 附錄A示範例題 張量概念 逆變矢量、協變矢量和張量 克羅內克符號δ 張量的基本運算 對稱張量和反對稱...
4.5 張量場絕對微分習題第5章 曲線坐標5.1 曲線坐標系5.2 曲線坐標局部對偶基5.3 協變(逆變)基底矢量導數5.4 曲線坐標系張量場分析...
§3.4 高階張量的協變導數 §3.5 張量方程 §3.6 梯度、散度、旋度 §3.8 黎曼-克里斯托費爾張量 §3.9 兩點張量場 第二篇 彈性力學基本方程 第四章 應力分...
5.2矢量的協變微分79 5.3張量的協變微分80 5.4協變微分法規則80 5.5不變微分運算元80 5.6內稟微分81 5.7相對張量81 習題演算82第...
包括張量的協變導數、微分,以及不變微分運算元:梯度、散度、旋度和拉普拉斯運算元,等等;第3章是張量在應變分析中的套用,簡單介紹張量在應變分析中的套用,主要包括位移、...
1.4.2協變與逆變轉換係數151.4.3矢量分量的坐標轉換關係161.4.4度量張量分量的坐標轉換關係161.5並矢與並矢式171.5.1並矢171.5.2縮並19...
它涉及到協變導數:給定流形某點的任一坐標表示,上述恆等式可以用黎曼曲率張量的分量形式表示為:第一(代數)比安基恆等式: 或等價地寫為...
設在一個n維單連通可微流形M上給定了黎曼度量G和一個三階對稱協變張量場A,若它們滿足一組所謂可積性條件,則存在一個從M到n+1維仿射空間A +‘的局部嚴格凸...
黎曼流形是一黎曼度量的微分流形.設M是n維光滑流形,若在M上給定一個光滑的二階協變張量場g,稱(M,g)為一個n維黎曼流形,g稱為該黎曼流形的基本張量或黎曼...
設M是希爾伯特微分流形,M上的黎曼度量指的是M上的一個連續的正定對稱二階協變張量場g。M連同其上給定的黎曼度量g稱為希爾伯特-黎曼流形,記為(M,g),這時,...
外微分形式,又稱微分形式,是微分流形上定義的反對稱協變張量場。...... 外微分形式,又稱微分形式,是微分流形上定義的反對稱協變張量場。中文名 外微分形式 ...
