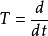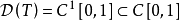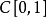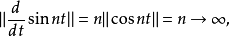基本介紹
定義,性質,套用-閉圖像定理,拓展,
定義
註:每個連續線性運算元T都可以將定義域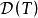 延拓到
延拓到 的閉包上,因此每個連續線性運算元T都可以看成是有閉定義域的,於是每個連續線性運算元必是閉運算元;但一般的閉線性運算元不一定是連續運算元(下面的例1證實了這一說法)。
的閉包上,因此每個連續線性運算元T都可以看成是有閉定義域的,於是每個連續線性運算元必是閉運算元;但一般的閉線性運算元不一定是連續運算元(下面的例1證實了這一說法)。
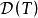

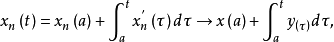
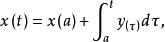

定義2(線性運算元的圖像)令T是定義在 上到Y的線性運算元,稱
上到Y的線性運算元,稱

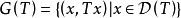
性質
上面定義的閉線性運算元有一個重要性質,即T的圖象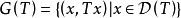 為乘積空間
為乘積空間 的一個閉線性子空間。定理描述為:
的一個閉線性子空間。定理描述為:
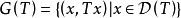

定理1 T是閉運算元的充分必要條件是 為閉集。
為閉集。

證明:(1)必要性 設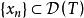 ,
,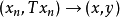 . 因為T是閉運算元,則
. 因為T是閉運算元,則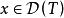 ,
, ,於是
,於是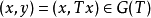 ,故
,故 是閉集。
是閉集。
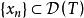
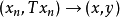
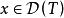

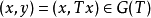

(2)充分性 設 是閉的,若
是閉的,若 ,那么
,那么



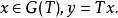
套用-閉圖像定理
證:該定理的證明參見參考文獻[1] 的291-292頁。
由定理1可知,定理2還可敘述成:在定理2的條件下,若T是閉運算元,則T是連續的。因此定義域是閉子空間的閉運算元是連續運算元。