函式的延拓:設E與F為兩個集合,P為E的子集,而f為從P到F中的映射. 任一從E到F中的映射,如果它在P上的限制為f,則稱該映射為f在E上的延拓。
解的延拓:不能繼續延拓的解稱為飽和解,飽和解的存在區間稱為解的最大存在區間。
基本介紹
函式的延拓
線性延拓



重要定理


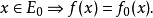
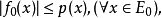
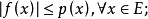
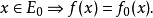

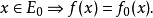


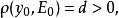
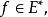

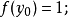
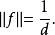
解的延拓
定義

舉例
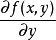

函式的延拓:設E與F為兩個集合,P為E的子集,而f為從P到F中的映射. 任一從E到F中的映射,如果它在P上的限制為f,則稱該映射為f在E上的延拓。
解的延拓:不能繼續延拓的解稱為飽和解,飽和解的存在區間稱為解的最大存在區間。





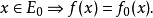
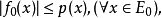
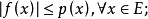
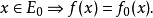

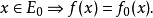


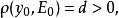
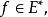

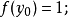
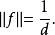

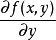
函式的延拓:設E與F為兩個集合,P為E的子集,而f為從P到F中的映射. 任一從E到F中的映射,如果它在P上的限制為f,則稱該映射為f在E上的延拓。解的延拓:...
函式的延拓就是把一個區間上的函式拓展到整個區間.方法是利用周期函式的性質,其中原區間的長度為一個周期。...
解析函式往往最初只在平面的某一限制區域中有定義,延拓的原則使我們能夠定義一個與它所在定義的任何特殊區域都無關的解析函式,它由原始函式與原始函式的全體延拓...
向上延拓(upward continuation)是計算其高度大於已知場高度的位場的過程。延拓涉及到格林定理的套用。如果較低面上的場是完全已知(對於重磁場一般為已知)和較低面...
向下延拓(downward continuation)是根據在某一水準面上的位場(例如重力場)測量值確定較低水準面上的位場值的過程。...
研究地球重力場的一種數學方法。地球外部重力場的延拓,主要是指由地面觀測數據計算空間某一高度的重力矢量,或由空間觀測數據計算地面上的重力矢量。前者稱為向上延拓...
,可改變f(x)在點x=0的定義,如果使之成為奇函式,按這種方法拓廣函式定義域的過程稱為奇延拓;如果使之成為偶函式,按這種方法拓廣函式定義域的過程稱為偶延拓。...
杜俊基延拓定理是蒂茨(Tietze,H.)關於實函式的延拓定理到無窮維空間中映射情形的一種推廣。...
反向延拓定理斷言:由滯後型泛函微分方程初值問題的提法,它總是沿正向(t≥σ)求解的,僅當方程滿足某些特定條件時,對某些初始函式可以進行負向延拓(t≤σ)。...
卡拉西奧多里-哈恩延拓定理是關於測度延拓的重要結果。數學上,測度(Measure)是一個函式,它對一個給定集合的某些子集指定一個數,這個數可以比作大小、體積、機率等等...
《非線性微分方程多解計算的搜尋延拓法》是2005年科學出版社出版的圖書,作者是陳傳淼。...
下調和延拓(subharmonic extension)使函式 保持下調和性的擴張.以下兩種情形有意義: 1.在R”中,若極集E為開集。的閉子集,u為 cu\E上定義的下調和函式且在...
《現代物理學的延拓》是1997年廣東教育出版社出版的圖書,作者是吳紫標。...... 《現代物理學的延拓》是1997年廣東教育出版社出版的圖書,作者是吳紫標。...
[磁異常延拓]continuation of magnetic anomaly; 根據某一面上已知的磁異常值,計算出空間任一點上相應的磁異常值的方法,在磁法勘探中習慣上統稱為磁異常的延拓。...
《煤炭資源整合管理及延拓戰略研究》是2011年出版的圖書,作者是肖亞寧。...... 《煤炭資源整合管理及延拓戰略研究》就我國煤炭資源的整合問題進行了理論及實證案例研究...
學科:地球物理勘探 詞目:位場解析延拓 英文:analytical continuation of potential fields 釋文:位場解析延拓是根據一個面上的一組位場數據確定另一個不同高度面...
解析延拓之後的ζ函式具有零點,他們分別是分布有序的平凡零點(所有負偶數),以及臨界帶 內的非平凡零點。以 表示虛部介於0與T之間的非平凡零點數量,則 遵循黎曼 -...
解析延拓,是數學上將解析函式從較小定義域拓展到更大定義域的方法。實質是定義域擴大的過程。透過此方法,一些原先發散的級數在新的定義域可具有迥異而有限的值。...
對理想採樣信號進行傅立葉變換,可以證明,理想採樣信號的頻譜是連續信號頻譜的周期延拓,重複周期為Ws(採樣頻率),即示例二 示例二 其中為理想採樣信號的頻譜,為連續...
