基本介紹
- 中文名:解析延拓
- 外文名:Analytic continuation
- 學科:數學
- 所屬領域 :函式論
- 相關概念:解析函式、解析等
定義
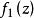
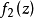
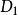


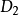

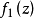



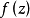
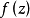


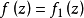


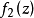



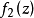
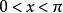





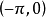
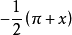
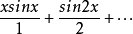





作為整體的解析函式的定義

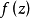
延拓的標準方法

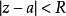
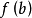



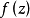






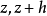


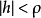

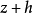

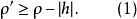

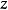






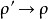


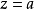
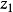
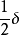
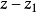




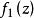
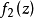
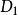


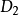

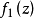



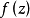
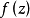


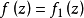


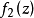



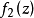
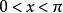





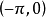
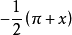
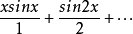






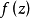

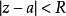
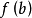



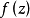






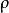
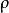
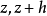


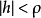

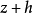

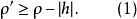

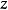






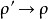


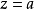
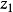
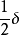
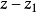



假定函式f1(z)與f2(z)分別在區域D1與D2中解析,D1與D2有一公共部分,在其上f1(z)=f2z)成立。於是將f1(z)與f2(z)在D1及D2內的全體點上的數值集合看...
解析延拓,是數學上將解析函式從較小定義域拓展到更大定義域的方法。實質是定義域擴大的過程。透過此方法,一些原先發散的級數在新的定義域可具有迥異而有限的值。...
解析開拓原理是擴大解析函式定義域的原理。解析延拓是數學上將解析函式從較小定義域拓展到更大定義域的方法。...
《圍岩力學分析中的解析方法》是1994年煤炭工業出版社出版的圖書。...... 7 解析延拓 8 半平面問題 9 單位圓圓域問題 10 受均布徑向壓力p圓盤的解 11 圓盤邊作...
學科:地球物理勘探 詞目:位場解析延拓 英文:analytical continuation of potential fields 釋文:位場解析延拓是根據一個面上的一組位場數據確定另一個不同高度面...
解析數論是數論中以分析方法作為研究工具的一個分支。解析數論是在初等數論無法解決的情況下發展起來的,如有了一個可以表達所有素數的素數普遍公式,一些由解析數論...
解析延拓之後的ζ函式具有零點,他們分別是分布有序的平凡零點(所有負偶數),以及臨界帶 內的非平凡零點。以 表示虛部介於0與T之間的非平凡零點數量,則 遵循黎曼 -...
黎曼-施瓦茲對稱原理亦稱黎曼-施瓦茲反射原理,是解析開拓的一種方法。...... 2 解析元素 3 解析延拓 黎曼-施瓦茲對稱原理簡介 編輯 黎曼-施瓦茲對稱原理是解析開拓...
由於伽瑪函式和下不完全伽瑪函式關於s,z都至少是亞純函式,上式可以自然地作解析延拓,並以此作為上不完全伽瑪函式的定義。下不完全伽瑪函式的多值性自然地導致上不...
可和到1/2。大部分可和法與相應冪級數的解析延拓相關,每個適當的可和法試圖描述的是序列趨於無窮時的平均表現,這種意義下也可以理解為無窮序列的均值。[2] ...
內容包括:複數與複變函數、解析函式、複變函數的積分、解析函式的冪級數表示法、解析函式的洛朗展式與孤立奇點、留數理論及其套用、共形映射、解析延拓和調和函式共...
*4.7解析延拓4.7.1解析延拓的概念4.7.2唯一性定理4.7.3解析延拓的方法習題4第5章 留數理論及其套用5.1留數及留數定理5.1.1留數的概念...
8.解析延拓的概念27.基本原理及其延拓28.單值性定理9.解析函式29.解析函式的概念30.初等函式31.奇點10.黎曼面的概念32.基礎方法...
《複分析導論·第1卷:單複變函數(第4版)》文字敘述極具特色,素材豐富。內容包括全純函式及其性質、解析延拓、幾何理論的基礎、解析方法、調和與次調和函式等。...
《複分析導論:多複變函數》是2008年高等教育出版社出版的圖書,作者是沙巴特。本書主要介紹了多變數全純函式、基本的幾何概念、解析延拓、亞純函式和留數等知識。...
