基本介紹
- 中文名:閉值域定理
- 外文名:Closed - field theorem
- 領域:數學
- 理論:巴拿赫空間理論
- 提出者:斯特凡巴拿赫
- 提出時間:1932年
人物簡介,巴拿赫空間,定理定義,
人物簡介
波蘭數學家。生於波蘭克拉科夫,卒於里沃夫。1910年進里沃夫工業學院學習之前主要靠自學,1914年因第一次世界大戰中斷學業。1916年與施坦因豪斯(Steinhaus,H.D.)相識,從此巴拿赫開始了他的研究生涯,並且兩人進行了合作研究,還在里沃夫形成了以他們兩人為中心的數學學派。1920年,他向里沃夫大學提交學位論文,並獲得博士學位。1920—1922年任里沃夫工業學院助教。1922年通過里沃夫大學講師資格考試,並成為該校“編外教授”,1927年成為正式教授。1929與施坦因豪斯創辦了《數學研究》,並同任主編。1939年任波蘭數學會主席。1939—1941年任里沃夫大學校長。1924年成為波蘭科學院通訊院士。他還是烏克蘭基輔科學院通訊院士。德軍占領期間,他曾在一個生產防傷寒疫苗的研究所做寄生蟲飼養員,並曾被德軍短期關押。波蘭解放後,他回到了里沃夫大學。
巴拿赫的主要貢獻是建立了賦范空間的概念,現稱為巴拿赫空間,他1922年正式發表的博士論文中首次提出了這一概念。他成功地在一般情況下把幾何與代數方法用於線性分析問題。1922—1923年,他又得到了壓縮映射的不動點定理、開映射定理。他在1929年給出了完備賦范線性空間上泛函延拓定理的推廣。他1932年出版的《線性運算元理論》和馮·諾伊曼(von Neumann,J.)的譜理論是泛函分析成為一個獨立的數學分支的標誌。該書中討論的弱收斂問題是局部凸拓撲線性空間理論的先導。在該書中,他還給出了完備賦范線性空間上連續線性運算元值域或是第一綱集,或是全空間,以及閉圖像定理等重要結果。他還在實變函式論、集合論、一般群論等方面有重要貢獻。他曾與他人合作得到了數列和函式序列的廣義極限理論、一般正交級數理論,還曾與塔爾斯基(Tarski,A.)合作提出了一個悖論。第二次世界大戰前,他與烏拉姆(Ulam,S.M.)等人在蘇格蘭咖啡館討論數學問題的記錄形成了“蘇格蘭書”,現保存在華沙巴拿赫國際數學中心。他曾於1932年獲里沃夫城市獎,1939年獲波蘭科學院獎。1967年,波蘭科學院數學研究所出版了他的文集。
巴拿赫空間
按範數導出的距離完備的賦范線性空間。設(X,‖·‖)為賦范線性空間。對x,y∈X,ρ(x,y)=‖x-y‖定義了X上的一個距離,使X成為度量空間.如果X按這個距離是完備的,就稱X為巴拿赫空間.L(Ω)(1≤p≤+∞),C(Ω),c,c0等都是巴拿赫空間的例子。
巴拿赫空間(含賦范空間)是1922年巴拿赫(Banach,S.)與維納(Wiener,N.)相互獨立提出的,並且在不到10年的時間內便發展為相當完美而又有多方面套用的理論。1932年,巴拿赫論述這部分理論的《線性運算元理論》一書的問世,是泛函分析作為獨立的數學分支出現的標誌。巴拿赫空間至今仍是泛函分析研究的基本對象之一。
定理定義
閉值域定理是數學中的巴拿赫空間理論中的一個定理,刻畫值域為閉的運算元的定理,給出了閉合稠定線性運算元(closed densely defined operator)的值域為閉集的充要條件。這一定理由斯特凡·巴拿赫於1932年在《線性運算元理論》(Théoriedes opérations linéaires)一文中給出了證明。
設X與Y為巴拿赫空間,若T:D(X)→Y是一個閉合的線性運算元,它的定義域D(X)在X中稠密,而是它的轉置運算元。則定理指出,如下五個結論等價:
結論一:R(T)是Y中的閉子空間。
結論二:R(T*)是X*中的閉子空間。
結論三:γ(T)=inf{‖Tx‖|x∈D(T),
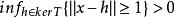
γ(T)稱為T的最小模,ker T為T的零空間。
結論四:R(T)={y∈Y|對所有的y*∈ker T*,都有y*(y)=0}。
結論五:R(T*)={x*∈X*|對所有的x∈ker T,都有x*(x)=0}。
以上所述匯總起來稱為閉值域定理。
