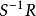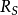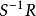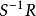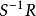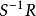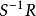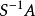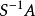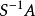局部化

局部化，是分式環的另一名稱，局部化有兩個重要性質，即保持正合性和諾特性質，通過哥爾迪(Goldie,A. W.)等人的工作，局部化方法已套用於非交換環論研究中.例如,哥爾迪證明了左諾特素環的(右)全分式環是單阿廷環.局部化方法有直觀的幾何背景.在代數幾何中研究一個代數簇在某點或某點附近的局部性質,而從各點的局部特性去把握代數簇的整體特性.這種方法在代數數論和整個代數學中是有效的方法.

基本介紹

• 中文名：局部化
• 外文名：localization
• 別名：分式環
• 性質：保持正合性和諾特性質
• 傑出人物：哥爾迪(Goldie,A. W.)等
• 套用領域：代數數論和整個代數學中

詳細介紹

分式環的造法以及與它相關聯的局部化方法大概是交換代數中最重要的技術性工具．它們相當於在代數幾何圖形里把注意力集中到一個開子集上或一點的近傍；這些概念的重要性是顯然的。

局部化，是分式環的另一名稱，分式環(fractional ring)全稱為“具有單位元的交換環R關於可乘子集S的分式環”．R的一個子集S若滿足：(1)R的單位元e∈S,(2)S關於乘法是封閉的．則稱S為可乘集．在集合

R×S={(r，s)|r∈R,s∈S}

中定義等價關係：(a,s)~(b,t)↔存在μ∈S,使(at—bs)μ=0．將(a，s)的等價類記為 ．在等價類所成集合中規定加法和乘法運算：

則該集合成環，稱為分式環．記作 或 ．一般R不能嵌入 中，但當S是R的所有非零因子集合時，R可以嵌入 中，這時 簡稱為R的分式環．若R還是整環。取S=R\{0}，則分式環 就是R的商域．又如R為整數環Z，p為素數，取S=R\(p)，則分式環 是所有表成既約分式時分母與p互素的有理數全體所成的環。

相關定理與性質

定理1 交換環R可嵌人到它的分式環A中，R中非零因子在A中有逆元。若R有非零因子，則A是含單位元的環。

性質：

1)設p是A的素理想． 那么它的補集S=A\p是乘法封閉的(事實上A\p是乘法封閉的↔P是素理想)． 這時將 寫作Ap．形如a/s的元素，這裡a∈p，組成A中一個理想m．如果b/t∉ m，那么b∉p，因此b∈S，於是b/t是Ap中可逆元．由此推出，如a是Ap中的理想而a⊈m，那么a就含一個可逆元，因而是整個環．因此，m是環An中僅有的極大理想；換句話說，Ap是局部環．從A轉化到Ap的過程叫做在p的局部化．

2) 是零環↔0∈S． ．

3)設f∈A而S={fⁿ)n>0．這時將寫作Af．

4)設a是A中任一理想，並且令S=1+a是一切1+x，x∈a，所成的集．顯然S是乘法封閉的．

更多內容請參考書籍《現代數學譯叢 交換代數導引》等。