基本介紹
例子
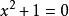
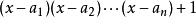

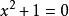
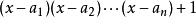
域F稱為代數閉域,如果對於任何係數屬於F的一元多項式f(x),f(x)在F中至少有一個根。...... 域F稱為代數閉域,如果對於任何係數屬於F的一元多項式f(x),f(...
在數學上,一個域F被稱作代數閉域,若且唯若任何係數屬於F且次數大於零的單變數多項式在F里至少有一個根。...
域是代數學的基本概念之一。即具有兩個運算的代數系。設F是至少含兩個元的集合,在F中定義了兩個二元運算:一個稱加法,使F成為加群,它的單位元稱為F的零元;...
代數封閉模型(algebraically closed model )是一種類似於代數閉域的模型。設U是理論T的模型,如果對U的每一個T擴張B,一切在BA中成立的存在語句也都在UA中成立,...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。代數閉群(algebraically closed group)是一類特殊的群。它將代數閉域...
代數對應(algebraic correspondence)是代數簇間的一種映射。設X和Y是兩個代數簇,X×Y的一個扎里斯基閉子集Z就給出了X與Y間的一個代數對應。...
若X→SpecR是有限型的,則稱X是R-代數的。設k是一個代數閉域,V是一個整的,可分的在k上代數的k-概型,則我們稱V是k上的一個代數簇。設(X,φ),(Y,...
半單性.群代數是半單的.半單環上的模.有限長度的半單環; Wedderburn定理.有限長度的單環與射影幾何基本定理.因式和 連續幾何.代數閉域上有限秩的半單代數...
完備域(perfect field)亦稱完全域。用可分性來刻畫的一類域一個域F,若它的每個代數擴張都是可分的,則稱F是完備域;否則,稱為不完備域。代數閉域、特徵為0的域...
光滑態射是光滑概形的相對化,也可看成是非異代數簇的族。設f:X→S是有限型態射,若f是平坦態射,並且對任一個點s∈S,纖維f-1(s)是剩餘域k(s)上的光滑...
為代數閉域 上的擬射影代數集, 為 上的代數集(即給定了態射 和 )。(1) 上的可逆層是平坦的。(2)開嵌入是平坦態射。(3)平坦態射的合成是平坦態射。(...
對單位根處的量子群和特徵p的代數閉域上的代數群,清楚具體地實現不可約表示。對量子群的基進行了系統的研究。這包括與Chari合作構造了量子群的單項基,計算了某些...
並將之廣為傳播,以作為代數幾何的問題中,只需稍多於微積分的知識就能闡述的一...令 為一特徵為零的代數閉域。若1、2、 是非零常數函式,(等價於以下條件:...
C域(C-field )一個概括代數閉域的重要概念.設F是一個域,若F上任意一個n元d次齊次方程,只要n>d`,在F中就有非零解,則稱F是個C域,i為。或正整數.代數...
希爾伯特零點定理(Hilbert's Nullstellensatz)是古典代數幾何的基石, 它給出了域 k 上的 n 維仿射空間中的代數集與域 k 上的 n 元多項式環的根理想的一一對應...
是某給定代數閉域 上非異擬射影簇的類,則對簇 上的有理等價環元類,有一個唯一的相交理論,滿足上面的A1-A7公理。證明:定理的證明中有兩個主要的成分。一個...
設K/F是一個域擴張,設A是K中在F上的代數元的全體,則A是K/F的中間域,稱F在K中的代數閉包。一個域K稱為是代數閉域,如果K〔x〕中每個次數大於零的多項式...
有理映射是代數簇上的有理函式概念的推廣。但是,它並不是集合意義下的映射。代數簇是代數幾何的基本研究對象。設k是一個域,域k上的代數簇就是一個整的、分離...
代數閉域上的任一解析空間是凝聚的。在這樣的空間(X,𝒪) 上的凝聚解析層的最重要的例子是局部自由層(即一局部同構於層 𝒪p的解析層)以及一解析集 的理想...
