基本介紹
- 中文名:雅可比猜想
- 外文名:Jacobian conjecture
- 分類:代數幾何、多項式
- 領域:數理科學
雅可比行列式,敘述,
雅可比行列式
F(c1, ... , cn)=(F1(c1, ... , cn), ... , Fn(c1, ... , cn))
函式F的雅可比行列式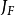 是由F的偏導數組成的n×n矩陣的行列式
是由F的偏導數組成的n×n矩陣的行列式
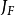

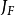
敘述
若F有反函式G: kn→kn,則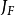 是非零的常數函式。
是非零的常數函式。
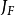
而其反命題則為雅可比猜想:
令 為一特徵為零的代數閉域。若
為一特徵為零的代數閉域。若

1、

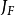

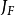
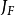


雅可比猜想(Jacobian conjecture)是多變數多項式的一個著名問題,最初是由數學家Keller於1939年提出,之後Shreeram Abhyankar取現名,並將之廣為傳播,以作為代數幾何的...
在向量微積分中,雅可比矩陣是一階偏導數以一定方式排列成的矩陣,其行列式稱為雅可比行列式。雅可比矩陣的重要性在於它體現了一個可微方程與給出點的最優線性逼近。...
世界三大數學猜想即費馬猜想、四色猜想和哥德巴赫猜想。費馬猜想的證明於1994年由英國數學家安德魯·懷爾斯(Andrew Wiles)完成,遂稱費馬大定理;四色猜想的證明於1976年...
《杜克數學學報》上發表的關於黎曼猜想的論文,和一篇1985年在中國讀書期間發在國內《數學學報》上的文章,而其關於“雅可比猜想”的博士論文則由於涉及的引理不能確認...
