基本介紹
- 中文名:閉域
- 外文名:closed field
例子
等價的刻劃
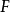
不可約多項式若且唯若一次多項式
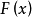
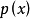
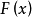
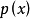
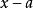
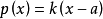
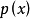
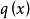
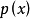
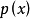
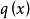
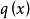
每一個多項式都是一次多項式的乘積
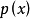
有理表達式的分解
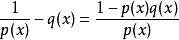
代數閉包
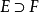
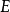
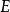
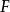
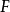
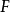
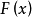
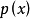
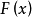
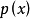
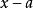
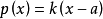
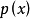
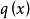
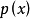
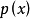
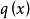
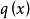
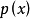
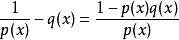
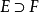
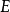
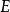
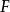
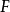
在數學上,一個域F被稱作代數閉域,若且唯若任何係數屬於F且次數大於零的單變數多項式在F里至少有一個根。...
閉域:開域連同其邊界.區域:開域,閉域或開域連同其一部分界點所成的點集.PS:通常來說,域指的是開域。參考資料:複變函數,史濟懷,劉太順編,中國科學技術大學...
上述用閉域套定理對有界閉域上二元連續函式的有界性定理進行證明,從一側面反映了此證明與用閉區間套定理證明閉區間上連續函式的有界性定理有異曲同工之妙,但...
完備域(perfect field)亦稱完全域。用可分性來刻畫的一類域一個域F,若它的每個代數擴張都是可分的,則稱F是完備域;否則,稱為不完備域。代數閉域、特徵為0的域...
希爾伯特零點定理(Hilbert's Nullstellensatz)是古典代數幾何的基石, 它給出了域 k 上的 n 維仿射空間中的代數集與域 k 上的 n 元多項式環的根理想的一一對應...
代數閉包(algebraic closure)是一個域的最大代數擴域。若域F的代數擴域Ω為代數閉域,則稱Ω為域F的一個代數閉包。一個域F的代數閉包總是存在的,並且在F同構...
阿廷定理(Artin theorem)實閉域上的多元多項式的重要定理.希爾伯特第17問題的正面解答和推廣.設F是一個實閉域,n為任一自然數,f(x)若對於F中任何一組元(a aZ...
C域(C-field )一個概括代數閉域的重要概念.設F是一個域,若F上任意一個n元d次齊次方程,只要n>d`,在F中就有非零解,則稱F是個C域,i為。或正整數.代數...
單連通域是直觀上沒有洞的平面區域的推廣,即區域內任何一條簡單閉曲線的內部沒有不屬於D的點。...
格林公式是一個數學公式,它描述了平面上沿閉曲線L對坐標的曲線積分與曲線L所圍成閉區域D上的二重積分之間的密切關係。一般用於二元函式的全微分求積。...
注:(1)閉區域雖然包含有邊界,但它也有可能是無界的;開區域是不含有邊界的,但它也可能為有界域。(2)開區域一定是開集,閉區域一定是閉集,而開集未必是開區域...
設k是一個代數閉域,A1=k,A1在(x,y)→x+y之下作成一個代數群,記作Ga。k*=A1\{0} 在(x,y)→xy之下作成一個代數群,記作Gm。域k上全體n×n可逆...
定義 德洛茲德定理(Drozd theore m)對代數的表示型進行分類的基本定理.設n是代數閉域K上的有限維代數,若對每一個維數d>0,存在有限個n-k葉]雙模從,且從...
設F是域K的子集,對於K的加法和乘法運算,F也做成一個域,則稱F是K的一個子域,K是F的一個擴域,記作K/F,稱K/F為一個域擴張。設,E/F和K/E都是域擴張...
