基本介紹
定義




形式定義
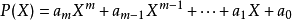




多項式的運算
環結構
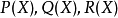


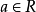
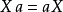


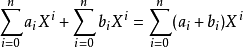
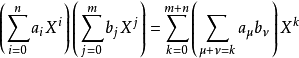
多項式的合成


求值


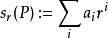
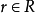
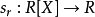
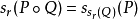
導數

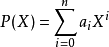



多變元的情形

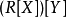

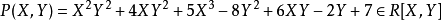







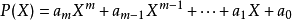




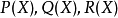


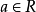
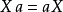


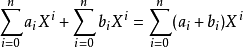
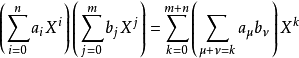




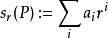
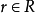
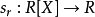
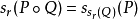

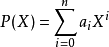




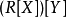

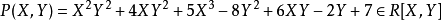


在抽象代數中,多項式環推廣了初等數學中的多項式。一個環 R 上的多項式環是由係數在R 中的多項式構成的環,其中的代數運算由多項式的乘法與加法定義。在範疇論的...
所有係數在數域P上的一元多項式的全體,稱為數域P上的一元多項式環,記為P[x],p稱為p[x]的係數域。一元多項式環具有通用性質。...
多元多項式(polynomial of several variables )是一元多項式的推廣,它是多項式理論研究的重要對象。有限多個單項式之和(假設其中不含同類項)稱為n元多項式,簡稱多項式...
多項式分裂域(splitting field of a polynomial )與多項式相關的一種域。在抽象代數中,具有域中係數的多項式分裂域是該域的最小域延伸,多項式在該域上分裂為線性...
霍爾多項式(Hall's polynomial)也稱哈爾多項式、Hall多項式,是對循環差集的一種刻畫,當G為v階循環群時,群環ZG與多項式環Z[x]/(xv-1)同構.若D={d1,d2,…...
的完全線性變換環,即F上的一個向量空間V的全部線性變換在變換的加法與乘法下構成的一個環;F上的多項式環,即F上一個或若干個文字的多項式全體構成的一個交換環...
歐氏環(Euclid ring)比主理想整環更窄的環類.它是整數環、域上一元多項式環有帶餘除法意義下的推廣。設R是整環,若存在R0=R-{ 0 }到非負整數集內的一個...
諾特環(Noetherian ring)是抽象代數中一類滿足升鏈條件的環。希爾伯特(Hilbert)首先在研究不變數理論時證明了多項式環的每個理想都是有限生成的,隨後德國數學家埃米·...
GCD環是一種有特殊性質的整環R,滿足其中任二個非零的元素都有最大公因數(GCD)。...... 若R是GCD環,其多項式環R[X1,...,Xn]也是GCD環。針對一個GCD環中...
在數學中,更具體地在抽象代數領域被稱為環形理論。諾特環(Noetherian ring)是抽象代數中一類滿足升鏈條件的環。希爾伯特(Hilbert)首先在研究不變數理論時證明了多項式...
整數環 。高斯整數環 。域上的多項式環( )與冪級數環(v(f) 定義為使 的最大非負整數 n)。離散賦值環, v(x)定義為使 的最大非負整數n,其中 表該...
pR=qlqz...qm,p; }q:是既約元,則必有n=m,且適當調換次序後對於i=1,2, w,n均有p與,相伴,則稱R為單一分解環.整數環、單一分解環上多項式環都是單...
諾特環是抽象代數中一類滿足升鏈條件的環。希爾伯特首先在研究不變數理論時證明了多項式環的每個理想都是有限生成的,隨後埃米·諾特從中提煉出升鏈條件,諾特環由此...
