霍爾多項式

霍爾多項式(Hall's polynomial)也稱哈爾多項式、Hall多項式，是對循環差集的一種刻畫，當G為v階循環群時，群環ZG與多項式環Z[x]/(x^v-1)同構.若D={d₁，d₂，…，d_k}為G的一個差集，則D的群環刻畫T(D)對應於Z[x]/(x^v-1)中的元θ(x)=x^d1+x^d2+...+x^dk，稱θ(x)為D的霍爾多項式。D為v階循環群中(v，k，λ)差集的充分必要條件是霍爾多項式適合θ(x)θ(x^-1)≡n+λT(x) (mod x^v-1)，式中T(x)=1+x+…+x^v-1，n=k-λ。

基本介紹

• 中文名：霍爾多項式
• 外文名：Hall's polynomial
• 所屬學科：數學
• 所屬問題：組合學（組合設計）
• 簡介：對循環差集的一種刻畫

基本介紹

用霍爾(Hall)多項式來刻劃-循環差集和研究差集之間的同構、等價關係時是比較方便的。

定義設

是模k剩餘的任一子集，則

叫做D的霍爾多項式。

例如，由CPPD(15，7，3)的

構成的(15，7，3)一循環差集

可以在mod 15的意義下寫為

然後用哈爾多項式表示為

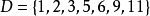
相關定理

定理 一個多項式

是一個-循環差集

的哈爾多項式的充要條件是

此處，且

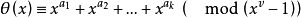
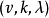
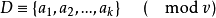
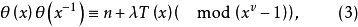
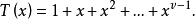
證 因

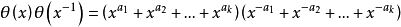
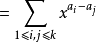
故(3)成立的充要條件是

此式成立的充要條件，就是D是一個-循環差集。

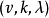
故得所證。

利用Hall多項式，可以構造生成差集碼的生成多項式。設

是一個2^s階的循環差集

令

及h(x)是θ(x)和的最大公約式，即

則長為n的差集碼定義為由下列生成多項式生成的循環碼

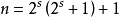
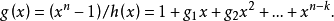
差集的刻畫

差集的刻畫是對差集的一種表征，按定義差集是群中的特殊子集，為討論問題方便起見，考慮阿貝爾群G的群環ZG，其中Z為整數環，則G中的差集D可用群環中元

來刻畫，若α為G的自同構，記

則G的k元子集D為差集的充分必要條件為，式中，

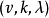
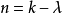
循環差集還可由霍爾多項式及循環序列來刻畫。以記循環加群Z_v中元，定義一個序列，使得i屬於循環差集D時，否則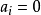，則稱該序列是循環差集D的特徵序列，一個長為v的(0，1)序列是一個(v，k，λ)循環差集的特徵序列的充分必要條件是和式

只取兩個值，當時值為k，而對別的j均取值λ，和式中下標i+j按模v簡化。循環差集的特徵序列刻畫法便於差集在數字通信理論中的套用。