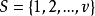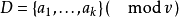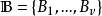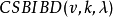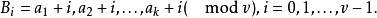基本介紹
- 中文名：循環差集
- 外文名：cyclic difference set
- 所屬學科：數學（組合學）
- 簡介：循環群中的差集
基本介紹,例題與相關定理,
基本介紹
設G為v階Abel群，其運算為加法，設D為G的一個k元子集，λ為給定正整數，若對G中任一非零元g，都有λ個序對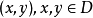
,使
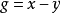,則稱D為Abel群G中的一個
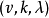-差集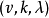 -difference set)。特別，當G為循環群時，稱D為G中的一個 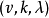-循環差集(cyclic difference set)。
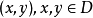
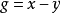
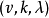
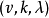
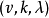
循環差集(Cyclic Difference Set)，有時也簡稱差集，是一種具有循環性質的對稱均衡不完全區組設計，用循環差集構造出來的碼具有循環特性，從而可以用循環移位暫存器構造編碼器和解碼器以簡化電路。
定義 以正整數v為模的k個互不同餘的整數所組成的集
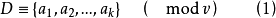
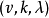
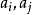
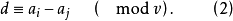
例題與相關定理
【例1】設v=13，則D={1，2，4，10}是一個(13，4，1)-循環差集。可以在模13意義下作如下驗證：
1≡2－1 5≡2－10 9≡10－1
2≡4－2 6≡10－4 10≡1－4 ‘
3≡4－1 7≡4－10 11≡2－4
4≡1－10 8≡10－2 12≡1－2
4個元素，它們兩兩的差值共有4(4－1)=12個，正好是上面所表示的1，2，…，12值。
【例2】設v=11，則D={2，6，7，8，10，11}是一個(11，6，3)-循環差集。
我們可以驗證模11下的差值如下：
1≡7－6≡8－7≡11－10
2≡8－6≡10－8≡2－11
3≡10－7≡11－8≡2－10
4≡6－2≡10－6≡11－7
5≡7－2≡11－6≡2－8
6≡8－2≡2－7≡6－11
7≡2－6≡6－10≡7－11
8≡10－2≡7－10≡8－11
9≡11－2≡6－8≡8－10
10≡6－7≡7－8≡10－11
循環差集與循環對稱均衡不完全區組設計有一一對應的關係，知道了循環差集的k個基本元素後，就可以將CSBIBD-的各區組寫出。我們從例2的差集D寫出11個區組
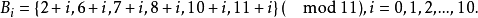
定理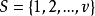
的一個k元集
