基本介紹
- 中文名:循環差集
- 外文名:cyclic difference set
- 所屬學科:數學(組合學)
- 簡介:循環群中的差集
基本介紹
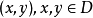
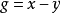
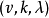
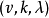
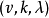
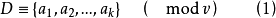
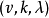
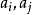
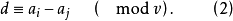
例題與相關定理
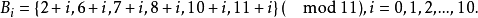
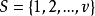
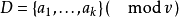
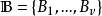
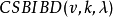
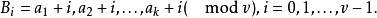

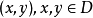
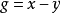
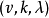
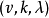
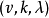
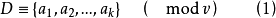
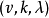
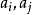
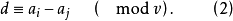
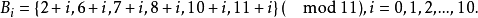
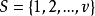
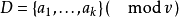
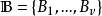
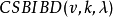
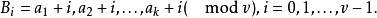
循環差集(cyclic difference set)是一類特殊差集,即循環群中的差集,例如,若循環加群Z15的元素記為{0,1,…,14},則D={0,1,2,4,5,8,10}是一個(15,7,...
e,如果 D 為 G 的 k(0<k<v) 元子集,且形如 xy-1(x,y∈D) 的元中含 G 的每個非單位元恰 𝝺 次,則稱 D 為 G 的一個(v,k,𝝺) 差集。...
平面差集(planar difference set)是一類組合構形,即(v,k,1)差集。若平面差集的階為n,則n=k-1,因此,平面差集為(n2+n+1,n+1,1)差集,n階平面差集的存在...
循環加集(cyclic addition set)是循環差集的一種推廣,設D={d₁,d₂,…,dk}為v階循環群Zv的k元子集,g為小於v的一個正整數,若對Zv中任一非零元s,...
辛格定理(theorem of Singer)是關於一類循環差集的存在性定理,該定理由辛格(J.Singer)於1938年利用有限射影幾何證得。...
霍爾多項式(Hall's polynomial)也稱哈爾多項式、Hall多項式,是對循環差集的一種刻畫,當G為v階循環群時,群環ZG與多項式環Z[x]/(xv-1)同構.若D={d1,d2,…...
乘子定理(multiplier theorem)用來判別差集乘子存在性的定理。...... 乘子定理說明,n的因數是乘子的重要來源.但這並不是惟一的來源.例如,11是(21,5,1)循環差...
乘子(multiplier)亦稱乘數,是一類特殊的自同構。設D為群G的一個(v,k,λ)差集,G的運算以加法記,α為G的一個自同構。若存在a,b∈G,使Dα=a+D+b,則稱...
循環設計的性質、變體和推廣 14.1 循環設計與循環差集的關係以及對二者的刻劃 14.2 存在性 14.3 乘數 14.4 循環擬差集 14.5 m-(v,k1,k2,...,km,λ...
