基本介紹
- 中文名:循環加集
- 外文名:cyclic addition set
- 簡介:循環差集的一種推廣
- 所屬學科:數學(組合學)
基本介紹,相關定理,
基本介紹
設D=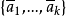 是Zv的一個k元子集,且g是整數,合0<g<v。
是Zv的一個k元子集,且g是整數,合0<g<v。
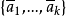
定義1如果D滿足條件:對Zv中任一元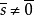 ,方程
,方程
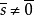


於是,個(v,k,λ,-1)-循環加集就是個(v,k,λ)-循環差集。
與循環差集的情況類似,對任意正整數v和 的循環加集很容易全部列出,故稱這些加集是平凡的,滿足
的循環加集很容易全部列出,故稱這些加集是平凡的,滿足

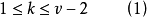
相關定理
定理1 若θ(x)為D的霍爾多項式,則D是(v,k,λ,g)循環加集的充分必要條件為
θ(x)θ(xg)≡β+λT(x) (mod xv-1), (2)
式中T(x)=1+x+…+xv-1,當1<k<v-1時,(v,k,λ,g)循環加集的參數滿足β=k2-λv,0≤β+λ≤k,0<λ<k及|β|<k,對於循環加集,也可以定義乘子,並且有類似於循環差集的乘子定理。
定理2對非平凡的(v,k,λ,g)-循環加集,有

定理3 若 ,則合gcd(g,v)>1的(v,k,λ,g)-循環加集都是平凡的。
,則合gcd(g,v)>1的(v,k,λ,g)-循環加集都是平凡的。

定理4 設D是一個(v,k,λ,g)-循環加集,且2|v,2不能整除g,則β是一個完全平方數。
系 設D是一個非平凡的(v,k,λ,g)-循環加集,且2|v,則β是一個完全平方數。
定理5 設D是一個非平凡的(v,k,λ,g)-循環加集,且β≠0,又設h是一個整數,合gcd(h,v)=1,那么,若且唯若gh是一個固定D的乘數時,D也是一個(v,k,λ,h)-循環加集。
定理6 若D是一個非平凡的(v,k,λ,g)-循環加集,且β≠0,則g2是固定D的一個乘數。
但是,這個定理對循環加集的非常重要的特款——循環差集,未能提供任何有用的結果,因為g=-1時,g2=1是一個循環差集的平凡的乘數。
有關循環加集的性質,類似於循環差集的乘數定理,以及某些類型的循環加集的構造方法等,已有不少有趣的結果。
值得一提的是,C.W.H.Lam證明了: 不存在非平凡的(v,k,λ,1)-循環加集。

