辛格定理

辛格定理(theorem of Singer)是關於一類循環差集的存在性定理，該定理由辛格(J.Singer)於1938年利用有限射影幾何證得。

基本介紹

• 中文名：辛格定理
• 外文名：theorem of Singer
• 所屬學科：數學（組合學）
• 所屬問題：組合學（組合設計理論）
• 簡介：關於一類循環差集的存在性定理

基本介紹

若q為素數冪，則存在

循環差集。

該定理由辛格(J.Singer)於1938年利用有限射影幾何證得，將有限域GF(q)上的n+1維非零向量x=(x₀，x₁，…，x_n)取作n維射影幾何的點，當b為GF(q)中非零元時，把bx與x看做相同的點，這些點的集合記為PG(n，q)，若ξ為擴域GF(qⁿ⁺¹)中的原根，則ξⁱ與ξ^j表示PG(n，q)中相同點的充分必要條件為i≡j(mod v)，這裡

於是，PG(n，q)中的所有點可表為ξ⁰，ξ¹，…，ξ^v-1.設y₁，y₂，…，y_n是GF(q)上n個線性無關的n+1維向量，把一切向量b₁y₁+b₂y₂+…+b_ny_n(式中b_i∈GF(q))所對應的點的集合稱為一個超平面，其中的點可表為 ，這裡

辛格證明：{d₁，d₂，…，d_k}是循環群Z_v中的(v，k，λ)差集，其中，λ=(q^n-1-1)/(q-1)。

辛格定理的證明

J.Singer於1938年引入了差集的概念並利用有限域上n維射影幾何中的超平面構作了一類重要的循環差集。

定理1(Singer)設q為素數冪，n≥2，又設

則存在Z_v中(v，k，λ)-差集， 使得由此差集的全體平移組成的循環對稱設計與以PG(n，q)中的點作元素，以超平面為區組所得到的SB(k，λ；v)同構。

證 設V為F_q上n+1維向量空間，則V的1維子空間便是PG(n，q)中的點，V的n維子空間便是PG(n，q)中的超平面。

設為F_q的n+1次擴域，α為的一個本原元，可看作F_q上的一個n+1維向量空間，它以1，α，...，αⁿ為一組基，取此空間作為V。

對，中的q-1個元素

都是F_q上方程x^q-1=1的根。由此它們就是F_q的全部非零元素，於是F_q中任一非零元t必可表成的形式,由此中兩個非零元αⁱ與α^j代表V中同一個1維子空間的充分必要條件是存在F_q中的元素t=使

亦即

於是

則便是V中全部1維子空間亦即PG(n,q)中全部v個點,映射

是PG(n,q)的一個自同構,σ生成一個v階循環群G=．G傳遞地作用在PG(n,q)中全體點的集合上,且G也傳遞地作用在全體超平面的集合上，由於,因此G在PG(n,q)中全體點的集合和全體超平面的集合上都是正則的.故若令D為由以全體超平面為區組,全體點為元素所組成的SB(k,λ；v)。則D是一個循環設計,令

則是Z_v中元素與PG(n,q)中的點之間的一個1-1對應,設S為PG(n,q)的一個超平面,令

則D便是Z_v中的一個(v,k,λ)-差集,由D的全體平移作區組所得的循環設計與D同構。

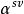
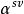
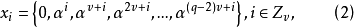
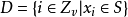
Singer定理所得到的差集叫Singer差集。