設 G 為 v 階乘法群,單位元為 e,如果 D 為 G 的 k(0<k<v) 元子集,且形如 xy-1(x,y∈D) 的元中含 G 的每個非單位元恰 𝝺 次,則稱 D 為 G 的一個(v,k,𝝺) 差集。當 G 為阿貝尓群(即交換群)成循環群時,分別稱 D 為阿貝尓差集或循環差集。
基本介紹
- 中文名:差集
- 外文名:difference set
- 適用範圍:數理科學
簡介

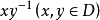
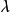
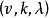
套用
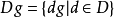
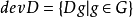
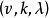
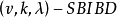
設 G 為 v 階乘法群,單位元為 e,如果 D 為 G 的 k(0<k<v) 元子集,且形如 xy-1(x,y∈D) 的元中含 G 的每個非單位元恰 𝝺 次,則稱 D 為 G 的一個(v,k,𝝺) 差集。當 G 為阿貝尓群(即交換群)成循環群時,分別稱 D 為阿貝尓差集或循環差集。

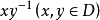
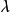
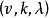
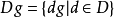
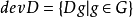
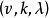
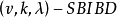
e,如果 D 為 G 的 k(0<k<v) 元子集,且形如 xy-1(x,y∈D) 的元中含 G 的每個非單位元恰 𝝺 次,則稱 D 為 G 的一個(v,k,𝝺) 差集。...
差集表(difference array)一種矩陣.設G(t>是t階加法群,A是元素屬於G (t)的}tXk階矩陣,如果A的任何兩列有序差遍歷G(t)的每個元素恰好久次,則稱A為G(t)...
平面差集(planar difference set)是一類組合構形,即(v,k,1)差集。若平面差集的階為n,則n=k-1,因此,平面差集為(n2+n+1,n+1,1)差集,n階平面差集的存在...
可分差集(divisible difference set)差集的一種推廣.若G為mn階群,具有n階正規子群N,D為G的k元子集,...
差集型正交表((difference OA)一類正交表.型如LuZ (tk >,其中t=p'(素數次冪),})2 (k=}t+1>的正交表稱為差集型正交表.由於它們的構造等同於差集表D(}...
梅農差集(Menon difference set)一類特殊參數的差集.梅農(Menon, P. K.)於1962年證明:若一個(二,k,}l)差集中二=4n,這裡n=k-}l,則這個差集的參數一定...
主條目:差集兩個集合也可以相"減"。A在B中的相對補集,寫作B−A,是屬於B的、但不屬於A的所有元素組成的集合。在特定情況下,所討論的所有集合是一個給定的...
在集合論 相對補集(差集)示意圖 和數學的其他分支中,存在補集的兩種定義:相對補集和絕對補集。1、相對補集若A和B 是集合,則A 在B 中的相對補集是這樣一個集合...
集合U和A的相對差集,符號為U \ A,是在集合U中,但不在集合A中的所有元素,相對差集{1,2,3} \ {2,3,4} 為{1} ,而相對差集{2,3,4} \ {1,2,3}...
乘子(multiplier)亦稱乘數,是一類特殊的自同構。設D為群G的一個(v,k,λ)差集,G的運算以加法記,α為G的一個自同構。若存在a,b∈G,使Dα=a+D+b,則稱...
辛格定理(theorem of Singer)是關於一類循環差集的存在性定理,該定理由辛格(J.Singer)於1938年利用有限射影幾何證得。...
乘子定理(multiplier theorem)用來判別差集乘子存在性的定理。...... 設D是二階阿貝爾群G的(二,k,.1)差集,m是n=k-.l的一個與v互素的因子,且m>}l.若整...
