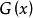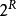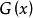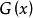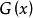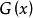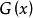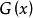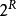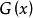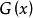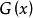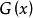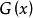生成多項式就是用來把要進行防錯處理的二進制碼流進行轉換生成校驗碼，然後接收方會收到原始的二進制碼流和校驗碼，按照與傳送方相同的多項式再次進行轉換生成校驗碼，與發來的校驗碼進行比較。如果一致則說明接收到的二進制碼流是正確的；反之則說明接收到的二進制碼流包含錯誤。
基本介紹
- 中文名：生成多項式
- 外文名：generator polynomial
- 套用領域：數學、物理
定義,位數,推論,生成原則,生成方法,生成步驟,舉例,
定義
若一個循環碼的所有碼字多項式都是一個次數最低的非零首一多項式 g(x)的倍式，則稱g(x)生成該碼，並稱g(x)為該碼的生成元或生成多項式。
生成多項式是接受方和傳送方的一個約定，也就是一個二進制數，在整個傳輸過程中，這個數始終保持不變。在傳送方，利用生成多項式對信息多項式做模2除生成校驗碼。在接收方利用生成多項式對收到的編碼多項式做模2除檢測和確定錯誤位置。
應滿足以下條件：
A、生成多項式的最高位和最低位必須為1。
B、當被傳送信息（CRC碼）任何一位發生錯誤時，被生成多項式做除後應該使餘數不為0。
C、不同位發生錯誤時，應該使餘數不同。
D、對餘數繼續做除，應使餘數循環。
位數
生成多項式位數 =CRC校驗碼位數 +1。注意有些生成多項式的簡記式中將生成多項式的最高位1省略了。
推論
（1）生成多項式的比特數越大，其差錯檢測能力越強；漏檢錯誤率越低。
（2） 生成多項式比特數相同的情況下，差錯檢測能力相同；漏檢錯誤率範圍大致相同，但是對於不同的信道誤碼率，又有不同的漏檢錯誤率。
生成原則
若設碼字長度為N，信息欄位為K位，校驗欄位為R位(N=K+R)，則對於CRC碼集中的任一碼字，存在且僅存在一個R次多項式g(x)，使得
V(x)=A(x)g(x)=xRm(x)+r(x);
其中: m(x)為K次原始的信息多項式， r(x)為R-1次校驗多項式（即CRC校驗和），
g(x)稱為生成多項式：
g(x)=g0+g1x1+ g2x2+...+g(R-1)x(R-1)+gRxR
傳送方通過指定的g(x)產生CRC碼字，接收方則通過該g(x)來驗證收到的CRC碼字。
結合系統的具體特點及要求，提出一種生成多項式的選取方法，其主要設計思想有以下兩個方面：
（1） 首先，為了確保選取的生成多項式校驗性能是最優的，考察在具體嵌入式網路系統中傳輸數據幀最大長度的情況下，碼重最大，漏檢率最低的生成多項式。
（2）其次，為了確保選取的生成多項式有較廣的使用範圍和良好的可移植性，分別考察小於和大於最大數據幀長度的情況，生成多項式的碼重及漏檢率的情況。
在這裡要注意的是嚴格按照這兩個方面的優先次序考慮，在保證自身套用環境中最優檢錯性能的前提下考察其擴展性和可移植性。
對於最小距離相同的生成多項式，要首先選取可檢測數據長度最大的生成多項式；對於較短的數據幀，如果要提高生成多項式的最小距離，必須以不影響該生成多項式對於長數據幀的校驗性能為前提；對於一些現行的協定，隨著網路的不斷發展，也會對協定進行修正，同時也會要求增加傳輸數據幀的長度，因此在選擇生成多項式時要考慮將來的可擴展性，使生成多項式傳輸較長數據幀時也能有較好的校驗性能。
生成方法
藉助於模2除法則，其餘數為校驗欄位。
例如：信息欄位代碼為: 1011001；對應m(x)=x6+x4+x3+1
假設生成多項式為：g(x)=x4+x3+1；則對應g(x)的代碼為: 11001
x4m(x)=x10+x8+x7+x4 對應的代碼記為：10110010000；
採用模2除法則: 得餘數為: 1010(即校驗欄位為：1010）
傳送方：發出的傳輸欄位為: 1 0 1 1 0 0 1 1010
信息欄位 校驗欄位
接收方：使用相同的生成碼進行校驗:接收到的欄位/生成碼（二進制除法）
如果能夠除盡，則正確，
給出餘數（1010）的計算步驟：
除法沒有數學上的含義，而是採用計算機的模二除法，即除數和被除數做異或運算。進行異或運算時除數和被除數最高位對齊，按位異或。
10110010000
^11001
--------------------------
01111010000
1111010000
^11001
-------------------------
0011110000
11110000
^11001
--------------------------
00111000
111000
^11001
-------------------
001010
則四位CRC校驗碼就為：1010。
利用CRC進行檢錯的過程可簡單描述為：在傳送端根據要傳送的k位二進制碼序列，以一定的規則產生一個校驗用的r位監督碼(CRC碼)，附在原始信息後邊，構成一個新的二進制碼序列數共k+r位，然後傳送出去。在接收端，根據信息碼和CRC碼之間所遵循的規則進行檢驗，以確定傳送中是否出錯。這個規則，在差錯控制理論中稱為“生成多項式”。
生成步驟
1、將X的最高次冪為R的生成多項式
轉換成對應的R+1位二進制數。
2、將信息碼左移R位，相當於對應的信息多項式
*
。
3、用生成多項式（二進制數）對信息碼做除，得到R位的餘數（注意：這裡的二進制做除法得到的餘數其實是模2除法得到的餘數，並不等於其對應十進制數做除法得到的餘數）。
4、將餘數拼到信息碼左移後空出的位置，得到完整的CRC碼。
【例】假設使用的生成多項式是=
。4位的原始報文為1010，求編碼後的報文。
解：
1、將生成多項式=轉換成對應的二進制除數1011。
2、此題生成多項式有4位（R+1）（注意：4位的生成多項式計算所得的校驗碼為3位，R為校驗碼位數），要把原始報文左移3（R）位變成1010 000
3、用生成多項式對應的二進制數對左移3位後的原始報文進行模2除（高位對齊），相當於按位異或：
1010000
1011
------------------
0001000
0001011
------------------
0000011
得到的余位011，所以最終編碼為：1010 011
舉例
名稱 生成多項式 簡記式* 套用舉例
CRC-4 x4+x+1 3 ITU G.704
CRC-8 x8+x5+x4+1 31 DS18B20
CRC-12 x12+x11+x3+x2+x+1 80F
CRC-16 x16+x15+x2+1 8005 IBM SDLC
CRC-ITU** x16+x12+x5+1 1021 ISO HDLC, ITU X.25, V.34/V.41/V.42, PPP-FCS,ZigBee
CRC-32 x32+x26+x23+...+x2+x+1 04C11DB7 ZIP, RAR, IEEE 802 LAN/FDDI,IEEE 1394,PPP-FCS
CRC-32c x32+x28+x27+...+x8+x6+1 1EDC6F41 SCTP
生成多項式的最高冪次項係數是固定的1，故在簡記式中，將最高的1統一去掉了，如04C11DB7實際上是104C11DB7。
備註：
（1）生成多項式是標準規定的
（2）CRC校驗碼是基於將位串看作是係數為0或1的多項式，一個k位的數據流可以看作是關於x的從k-1階到0階的k-1次多項式的係數序列。採用此編碼，傳送方和接收方必須事先商定一個生成多項式，其高位和低位必須是1。要計算m位的幀M(x)的校驗和，基本思想是將校驗和加在幀的末尾，使這個帶校驗和的幀的多項式能被除盡。當接收方收到加有校驗和的幀時，用去除它，如果有餘數，則CRC校驗錯誤，只有沒有餘數的校驗才是正確的。
