定義
若以(n,k,m)來描述卷積碼,其中k為每次輸入到卷積編碼器的bit數,n為每個k元組碼字對應的卷積碼輸出n元組碼字,m為編碼存儲度,也就是卷積編碼器的k元組的級數,稱m+1= K為編碼約束度m稱為約束長度。卷積碼將k元組輸入碼元編成n元組輸出碼元,但k和n通常很小,特別適合以
串列形式進行 傳輸,時延小。與
分組碼不同,卷積碼編碼生成的n元組元不僅與當前輸入的k元組有關,還與前面m-1個輸入的k元組有關,編碼過程中互相關聯的
碼元個數為n*m。卷積碼的糾錯性能隨m的增加而增大,而
差錯率隨N的增加而
指數下降。在
編碼器複雜性相同的情況下,卷積碼的性能優於分組碼。
 卷積碼的編碼器
卷積碼的編碼器介紹
一種卷積碼編碼器
卷積碼是1955年由Elias等人提出的,是一種非常有前途的編碼方法。我們在一些資料上可以找到關於分組碼的一些介紹,分組碼的實現是將編碼信息分組單獨進行編碼,因此無論是在編碼還是解碼的過程中不同碼組之間的碼元無關。
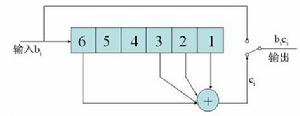 一種卷積碼編碼器
一種卷積碼編碼器根本區別
卷積碼和分組碼的根本區別在於,它不是把信息序列分組後再進行單獨編碼,而是由連續輸入的信息序列得到連續輸出的已
編碼序列。即進行分組編碼時,其本組中的n-k個校驗元僅與本組的k個信息元有關,而與其它各組信息無關;但在卷積碼中,其編碼器將k個信息碼元編為n個碼元時, 這n個碼元不僅與當前段的k個信息有關,而且與前面的(m-1)段信息有關(m為編碼的約束長度)。
有關信息
同樣,在卷積碼解碼過程中,不僅從此時刻收到的碼組中提取
解碼信息,而且還要利用以前或以後各時刻收到的碼組中提取有關信息。而且卷積碼的糾錯能力隨約束長度的增加而增強,
差錯率則隨著約束長度增加而呈指數下降。
約束關係
卷積碼(n,k,m) 主要用來糾隨機錯誤,它的碼元與前後碼元有一定的約束關係,編碼複雜度可用編碼約束長度m*n來表示。一般地,最小距離d表明了卷積碼在連續m段以內的距離特性,該碼 可以在m個連續碼流內糾正(d-1)/2(向下取整)個錯誤。
 狀態圖
狀態圖解碼方式
卷積碼的糾錯能力不僅與約束長度有關,還與採用的解碼方式有關。總之,由於n,k較小,且利用了各組之間的
相關性,在同樣的碼率和設備的複雜性條件下,無論理論上還是實踐上都證明:卷積碼的性能至少不比分組碼差。
編碼原理
卷積碼編碼器
以二元碼為例,
編碼器如圖。輸入信息序列為u=(u0,u1,…),其多項式表示為u(x)=u0+u1x+…+ulxl+…。編碼器的連線可用多項式表示為g(1,1)(x)=1+x+x2和g(1,2)(x)=1+x2,稱為碼 的子生成多項式。它們的係數矢量g(1,1)=(111)和g(1,2)=(101)稱作碼的子生成元。以子
生成多項式為陣元構成的多項式
矩陣G(x)=[g(1,1)(x),g(1,2)(x)],稱為碼的生成多項式矩陣。
 狀態圖2
狀態圖2生成矩陣
由生成元構成的半無限矩陣稱為碼的
生成矩陣。其中(11,10,11)是由g(1,1)和g(1,2)交叉連線構成。編碼器輸出序列為c=u·G,稱為碼序列,其多項式表示為c(x),它可看作是兩個子碼序列c⑴(x)和c⑵(x)經過合路開關S合成的,其中c⑴(x)=u(x)g(1,1)(x)和c⑵(x)=u(x)g(1,2)(x),它們分別是信息序列和相應子生成元的
卷積,卷積碼由此得名。
 矩陣圖
矩陣圖在一般情況下,輸入信息序列經過一個時分開關被分成k0個子序列,分別以u(x)表示,其中i=1,2,…k0,即u(x)=[u(x),…,u(x)]。編碼器的結構由k0×n0階生成多項式矩陣給定。輸出碼序列由n0個子序列組成,即c(x)=[c(x),c(x),…,c(x)],且c(x)=u(x)·G(x)。若m是所有子生成多項式g(x)中最高次式的次數,稱這種碼為(n0,k0,m)卷積碼。
表示方法
多項式法
描述卷積碼編碼器過程的方法有很多,如矩陣法、多項式、碼樹和
格線圖等,這裡我們主要介紹和卷積碼編碼器結構密切相關的多項式法,以及與卷積碼解碼密切相關的格線圖法。
結構圖 多項式法就是由卷積碼的生成多項式直接得出其編碼器的結構圖。如前面例子中的(2,1,2)卷積碼的生成多項式矩陣為:G(D)=[1
,1
]
 卷積碼狀態圖
卷積碼狀態圖 其中,D是延遲運算元,生成多項式的第一項為1 D
,表示輸出編碼的第一個碼元等於輸入碼元x(n)與前兩個時刻輸入的碼元x(n-1)、x(n-2)的模2和,同理第二項類似。
卷積碼
將編碼器暫存器中的內容組合(x(n-1)、x(n-2))定義為編碼器狀態。如仍以前面所舉的例子(2,1,2)為例,則該編碼器的狀態有四種:00,10,01和11,下面分別用a,b,c,d來代替。編碼器在每一個
時鐘沿打入一個輸入信息x(n),因此圖示
暫存器組合內容就變為(x(n),x(n-1))即狀態發生了轉移,並同時輸出G0(n)、G1(n)。由此我們可以將圖所示編碼過程用右圖所示的
狀態圖表示。
編碼器
由圖所示,隨著信息序列不斷輸入,編碼器就不斷從一個狀態轉移到另一個狀態並同時輸出相應的碼序列,所以圖3所示狀態圖可以簡單直觀的描述
編碼器的編碼過程。因此通過狀態圖 很容易給出輸入信息序列的編碼結果,假定輸入序列為110100,首先從零狀態開始即圖示a狀態,由於輸入信息為“1”,所以下一狀態為b並輸出“11”,繼續輸入信息“1”,由圖知下一狀態為d、輸出“01”……其它輸入信息依次類推,按照狀態轉移路徑a->b->d->c->b->c->a輸出其對應的編碼結果“110101001011”。
 格線圖
格線圖格線圖
狀態圖可以完整的描述編碼器的工作過程,但是其只能顯示狀態轉移的過程而不能顯示狀態轉移發生的時刻,由此引出用來表示卷積碼的另一種常用方法——
格線圖。格線圖就是時 間與對應狀態的轉移圖(如圖),在格線圖中每一個點表示該時刻的狀態,狀態之間的連線表示狀態轉移。通過觀察格線圖可以發現格線圖中輸入信息x(n)並沒有標出,但如觀察到轉移後的狀態表示(x(n),x(n-1))就可以發現輸入信息已經隱含在轉移後的狀態中。在圖中還可以發現兩個格線圖不同主要集中在轉移後狀態位置不同。重新排序結構(即所謂蝶型結構)是為了最佳化運算而設計的,因為其中蝶型與蝶型之間是相互獨立的。
 維特比解碼過程
維特比解碼過程過程
下面就讓我們來看看格線圖是如何描述卷積編碼過程的:仍以(2,1,2)為例,假定輸入序列為1011010100,起始狀態(零時刻)為狀態a(零狀態)。第一個有效時鐘沿來臨後,編碼器接收到輸入信息“1”,根據圖所示格線圖知該時刻(即時刻1)狀態為b,並輸出其對應的編碼結果“11”,同樣在下一個時刻(時刻2)接收到輸入信息“0”,狀態變為c並輸出“10”,接下來的輸入數據依次類推……,由此我們可以用格線圖作出該例子的卷積編碼過程,如圖5所示,其中兩個狀態連線之間的信息為輸出結果。
 暫存器
暫存器解碼方法
其中和。這裡“+”為模 2 運算(q=p元碼按模p運算)。解碼就是根據
編碼規則和信道干擾的統計特性,對信息序列u(x)作出估值的方法。常用的有三類解碼方法,即代數解碼、
維特比解碼和序貫解碼。
⒈代數
代數解碼是將卷積碼的一個編碼約束長度的碼段看作是[n0(m+1),k0(m+1)]
線性分組碼,每次根據(m+1)分支長接收數字,對相應的最早的那個分支上的信息數字進行估計,然後向前推進一個分支。上例中信息序列 =(10111),相應的碼序列 c=(11100001100111)。若接收 序列R=(10100001110111),先根據R的前三個分支(101000)和碼樹中前三個分支長的所有可能的 8條路徑(000000…)、(000011…)、(001110…)、(001101…)、(111011…)、(111000…)、(110101…)和(110110…)進行比較,可知(111001)與接收序列(101000)的距離最小,於是判定第 0分支的信息數字為 0。然後以R的第 1~3分支數字(100001)按同樣方法
判決,依此類推下去,最後得到信息序列的估值為=(10111),遂實現了糾錯。這種解碼法,解碼時採用的接收數字長度或解碼約束長度為(m+1)n0,所以只能糾正不多於(dmin-1)/2個錯誤(n長上的)。實用中多採用反饋擇多邏輯解碼法實現。
 衛星
衛星⒉維特比
維特比解碼過程
維特比解碼是根據接收序列在碼的格圖上找出一條與接收序列距離(或其他量度)為最小的一種算法。它和
運籌學中求最短路徑的算法相類似。若接收序列為R=(10100101100111),解碼器從某個狀態,例如從狀態ɑ出發,每次向右延伸一個分支(對於l<L,從每個節點出發都有 2=2種可能的延伸,其中L是信息序列段數,對l≥L,只有一種可能),並與接收數字相應分支進行比較,計算它們之間的距離,然後將計算所得距離加到被延伸路徑的累積距離值中。對到達每個狀態的各條路徑(有2=2條)的距離累積值進行比較,保留距離值最小的一條路徑,稱為倖存路徑(當有兩條以上取最小值時,可任取其中之一),解碼過程如圖。圖中標出到達各級
節點的倖存路徑的距離累積值。對給定 R的估值序列為=(10111)。這種算法所保留的路徑與接收序列之間的似然機率為最大,所以又稱為最大似然解碼。這種解碼的解碼 約束長度常為編碼約束長度的數倍,因而可以糾正不多於(df/2)個錯誤。
 回溯法TB
回溯法TB ⒊ 序貫解碼
序貫解碼是根據接收序列和編碼規則,在整個碼樹中搜尋(既可以前進,也可以後退)出一條與接收序列距離(或其他量度)最小的一種算法。由於它的解碼器的複雜性隨m值增大而線性增長,在實用中可以選用較大的m值(如20~40)以保證更高的可靠性。許多深空和
海事通信系統都採用序貫解碼。
描述及最佳化
Viterbi 解碼示例
卷積碼的Viterbi 解碼是根據接收碼字序列尋找編碼時通過格線圖最佳路徑的過程,找到最佳路徑即完成了解碼過程,並可以糾正接收碼字中的錯誤比特。Viterbi 解碼算法步驟如下描述:
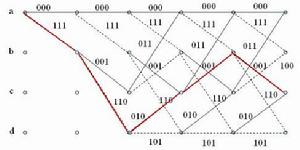 Viterbi 解碼示例
Viterbi 解碼示例①根據接收碼符號R,計算出相應的分支量度值BM(R/ Cj),j = 1 、2 ;
②進入某一狀態的2 條分支量度BM (R/ Cj)與其前狀態路徑量度PM累加求和;
③比較到達當前狀態的2 條新的路徑量度PM的大小,選擇最大者作為新的狀態路徑量度存儲起來,並保存與此路徑對應的碼字;
④對所有的256 個狀態都實施上述加、比、選(
ACS) 運算;
⑤在每一解碼時刻,滿足延時就從256 條留存路徑中,選擇路徑量度最大的一條路徑作為解碼數據輸出;
⑥進入下一解碼時刻,重複以上步驟,直至解碼結束。
由於卷積碼解碼的複雜度隨著約束長度的增加以非線性方式迅速增加,在實際套用中,卷積碼的實際套用性能往往受限於存儲器容量和系統運算速度,尤其是對約束長度比較大的卷積碼。為了在有限的
硬體或
軟體資源條件下保證系統較高的解碼性能,下面對算法進行最佳化。
⒈ 留存路徑更新算法最佳化
傳統的實現留存路徑存儲器(SMU) 更新的算法,有暫存器交換法RE 和
回溯法TB ,其詳細內容請參考有關文獻。暫存器交換法利用數據在暫存器中不斷交換,來更新留存路徑,實現信息的解碼,相對於TB 法不斷讀寫存儲數據和需要延時回溯判決,其優點是
存儲單元少、解碼延時短。RE 方法的缺點是內聯關係過於複雜,不適契約束長度比較大的卷積碼解碼器的
FPGA實現。基於RE 提出了對留存路徑存儲及輸出最佳化的實現方法,具體描述如下:.
具體描述
①逐狀態分配256 個存儲器單元,單元位數由延時D (解碼深度) 決定,每單元存儲一個碼字;
②每一個狀態當前留存路徑存儲器的值由選定的前一狀態存儲器值和路徑對應的碼字決定(見上述Viterbi 解碼算法步驟描述③) ;
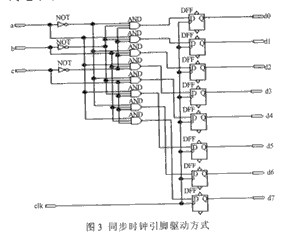 解碼深度
解碼深度③每一個解碼時刻只向存儲單元中存人留存路徑的碼字,並把選定碼字寫入存儲單元中最低位;
④當解碼時刻大於延時D 時,判決出當前時刻的所有狀態中具有最大路徑量度的狀態,並將其對應的留存路徑存儲單元中的最高位作為解碼結果輸出;
⑤在實現存儲單元的移位時,可採用
循環移位的方式,避免重複讀寫,在軟體實現時如果採用
指針的方式讀寫地址,也可以做到只用一套存儲器,這樣就能繼續在節省空間和提高運算速度上更進一步,在
Matlab仿真中由於系統本身的特點,只須用簡單的命令完成以上操作。
由於留存路徑存儲器中存入的只是路徑信息,因而節省了存儲空間;當解碼輸出時,唯讀出具有最大路徑量度的狀態所對應的留存路徑存儲單元最高位即可,不須向前回溯,減少了讀
RAM的次數(由D次減少至1 次) 提高了解碼速度。
⒉最佳化判決
在輸出時需要做延時判斷,以確定延時足夠再輸出正確數據。但每一時刻做延時的後果是增加了運算量,導致系統效率較低,根據仿真實現的特點,可以做以下修改:為了避免重複做延時判斷,節省運算量,解碼輸出時省略這一判斷,每一時刻都有判決輸出碼字,只是在接收解碼數據時把開始D時刻的接收
碼字丟棄, 相當於解碼單元從D時刻開始輸出,這是一種把部分系統功能從複雜模組轉移分離到相對簡單模組的思想。相對於在解碼過程不斷重複做判斷,這種做法無論在軟體或者硬體實現中,都能一定程度上提高運算速度。
 解碼深度圖
解碼深度圖 卷積碼的編碼器
卷積碼的編碼器 一種卷積碼編碼器
一種卷積碼編碼器 狀態圖
狀態圖 狀態圖2
狀態圖2

 卷積碼狀態圖
卷積碼狀態圖
 格線圖
格線圖 維特比解碼過程
維特比解碼過程 暫存器
暫存器 衛星
衛星 回溯法TB
回溯法TB Viterbi 解碼示例
Viterbi 解碼示例 解碼深度
解碼深度 解碼深度圖
解碼深度圖
 卷積碼的編碼器
卷積碼的編碼器 一種卷積碼編碼器
一種卷積碼編碼器 狀態圖
狀態圖 狀態圖2
狀態圖2

 卷積碼狀態圖
卷積碼狀態圖
 格線圖
格線圖 維特比解碼過程
維特比解碼過程 暫存器
暫存器 衛星
衛星 回溯法TB
回溯法TB Viterbi 解碼示例
Viterbi 解碼示例 解碼深度
解碼深度 解碼深度圖
解碼深度圖