基本介紹
基本介紹

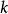

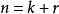
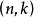
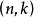
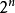
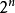
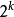

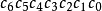
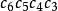
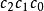
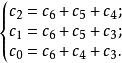
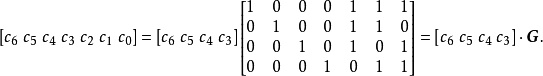
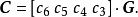
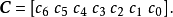
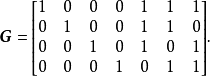

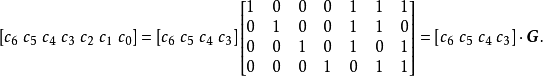
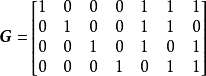
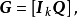

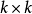
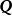
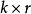

重要特性



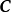
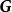
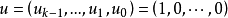

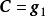
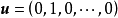
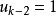
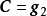





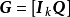
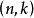
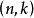
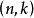
與監督矩陣H的關係

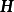

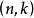
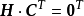
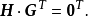
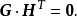
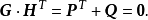
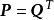
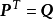

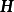

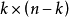
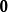
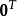

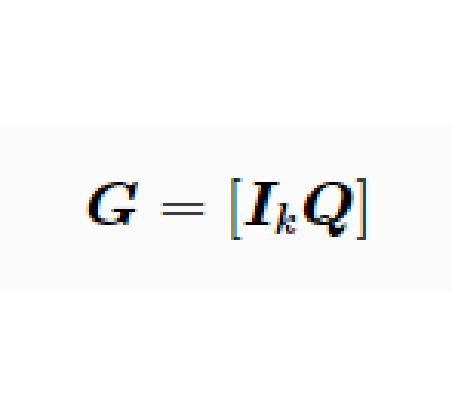

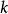

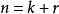
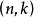
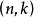
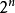
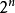
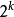

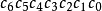
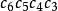
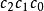
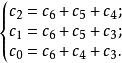
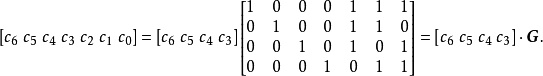
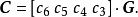
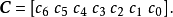
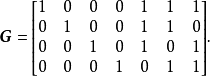

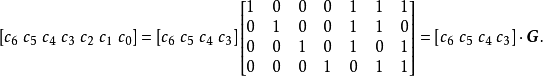
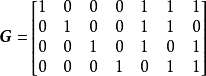
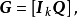

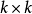
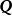
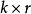




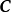
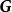
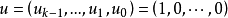

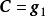
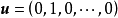
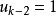
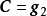





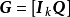
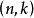
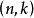
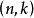

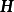

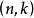
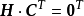
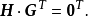
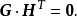
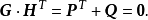
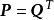
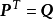

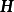

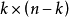
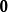
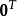

生成矩陣是線性碼的一種表示。e元[n,a]線性碼C的一個生成矩陣是有限域Fₑ上的一個a×n矩陣,其行向量構成子空間C的一組基,設C與C′是兩個e元線性碼,G...
旋轉矩陣(英語:Rotation matrix)是在乘以一個向量的時候有改變向量的方向但不改變大小的效果並保持了手性的矩陣。旋轉矩陣不包括點反演,點反演可以改變手性,也就是...
魔方矩陣又稱幻方,是有相同的行數和列數,並在每行每列、對角線上的和都相等的矩陣。魔方矩陣中的每個元素不能相同。你能構造任何大小(除了2x2)的魔方矩陣。...
零矩陣,在數學中,特別是線上性代數中,零矩陣即所有元素皆為0的矩陣。在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及...
希爾伯特矩陣是一種數學變換矩陣,正定,且高度病態(即,任何一個元素髮生一點變動,整個矩陣的行列式的值和逆矩陣都會發生巨大變化),病態程度和階數相關。...
編碼矩陣(code matrix):數字遙控系統中解碼器的一個組成部分。由雙穩態觸發器和編碼開關組成。每個雙穩態有“1”和“2”兩種狀態,n個雙穩級聯起來就有2n種可能...
T矩陣(T-matrix)是一類特殊的矩陣,可用於構作鮑默特-霍爾表,若G={g1,g2,…,gn}為加法可換群,X⊆G,M=(mij),當gj-gi∈X時mij=1,否則mij=0,則稱...
由於套用方便的需要形成了信號矩陣切換,所以說在每個信號階段都有相應的矩陣切換...計算機內部以數字方式生成的顯示圖像信息,被顯示卡中的數字/模擬轉換器轉變為R、G...
在數學和數學物理中,泡利矩陣是一組三個2×2的么正厄米復矩陣,以物理學家沃爾夫岡·泡利命名的。在量子力學中,它們出現在泡利方程中描述磁場和自旋之間相互作用的...
托普利茲矩陣,簡稱為T型矩陣,它是由Bryc、Dembo、Jiang於2006年提出的。托普利茲矩陣的主對角線上的元素相等,平行於主對角線的線上的元素也相等;矩陣中的各元素...
蛇形矩陣(Snake matrix)是矩陣的一種,常被套用在編程題目與數學數列中,需要提取每條斜線里最小的數字,處理代碼為@echo off&set c=9。...
多特質-多方法矩陣是利用多種不同形式和內容的測驗或其它測評手段進行多種特質的測量,並計算出不同測評結果之間的相關,生成相關關係數矩陣的測量方法。多特質-多...
矩陣切換器就是將一路或多路視音頻信號分別傳輸給一個或者多個顯示設備,如兩台電腦主機要共用一個顯示器,矩陣切換器可以將兩台電腦主機上的內容任意到同一個或多...
Gell-Mann矩陣實際就是上是SU(3)群特定選取的一組生成元(李代數)的特定基礎表示。所謂“特定選取”是指這些矩陣的正交性(至多差一個歸一化因子)。也就是說以...
矩陣切換器就是將一路或多路視音頻信號分別傳輸給一個或者多個顯示設備,如兩台電腦主機要共用一個顯示器,矩陣切換器可以將兩台電腦主機上的內容任意切換到同一個...
波斯頓矩陣(又稱四象限分析法、產品系列結構管理法、波士頓諮詢集團法等),是由美國著名的管理學家、波士頓諮詢公司創始人布魯斯·亨德森於1970年首創的一種用來分析和...
卷積碼生成矩陣 編輯 由生成元構成的半無限矩陣稱為碼的生成矩陣。其中(11,10,11)是由g(1,1)和g(1,2)交叉連線構成。編碼器輸出序列為c=u·G,稱為碼序列...
Toeplitz矩陣...... toeplitz(x)用向量x生成一個對稱的托普利茲矩陣。例如:T=toeplitz(1:6)Toeplitz英文例句 編輯 1.Slant ToeplitzOperators on Bergman SpaceBergma...
