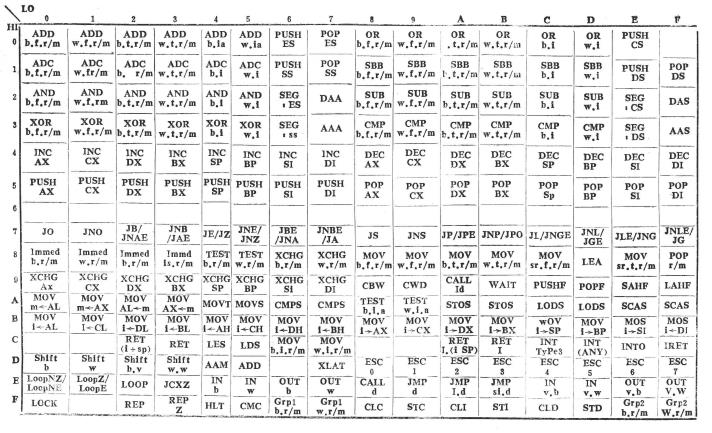
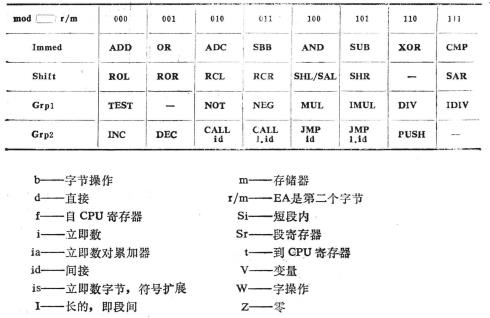
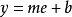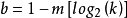定義
編碼矩陣(code matrix):數字遙控系統中
解碼器的一個組成部分。由雙穩態觸發器和編碼開關組成。每個雙穩態有“1”和“2”兩種狀態,n個雙穩級聯起來就有2
n種可能的組合,每一種組合即為二進制碼組,編碼開關按二進制碼組連線。編碼矩陣的用途是將指令(操作鍵的位置)變換成電信號。
所謂矩陣電路,是一種能將幾路輸入信號各按一定比例線性相加/減而得到一個或幾個不同輸出信號的電路。在彩色電視播送端的視頻通道中,需要將R、G、B基色信號變換成Y、R-Y、B-Y信號,其變化關係為
這種運算屬矩陣運算,故稱實現上式運算的電路為編碼矩陣電路。矩陣電路可由無源網路組成,也可由有源網路組成,最簡單的編碼矩陣電路是無源電阻矩陣電路。使用電阻矩陣電路時要求信號源的內阻、矩陣輸出電阻都必須遠小於矩陣電阻,下圖示出了有三路輸入、一路輸出的電阻矩陣電路。
 電阻矩陣電路
電阻矩陣電路上圖中,E1、E2、E3為信號源,R1、R2、R3為矩陣電阻,R0為矩陣輸出電阻。如果要求E1、E2、E3按k1:k2:k3的比例形成輸出信號電壓E0,而且電路滿足上述電阻矩陣電路的基本要求,則由上圖可得出以下關係:
式中,
為以常數。這時,E
1、E
2、E
3便以
:
:
的比例組合稱輸出信號E
0,即 k
1:k
2:k
3=
:
:
,式中,k
1、k
2、k
3為矩陣係數。
上圖中若E
1為基色信號R,E
2為基色信號G、E
3為基色信號B,且選擇
:
:
=0.30:0.59:0.11時,其輸出即為亮度信號Y。可見,三個矩陣電阻數值完全決定了三路信號混合的比例係數(矩陣係數),與R
0無關,因此,稱為矩陣電阻。
若用此矩陣電路形式組成色差信號R-Y時,使
:
:
=0.70:0.59:0.11,同時在G、B信號的輸人通路中各加入一個倒相器;組成色差信號B-Y時,使
:
:
=0.70:0.59:0.11,同時在R、G信號的輸入通路中各加入一個倒相器。
編碼矩陣的設計
多個方法可用於將一個多類問題分解為多個二分類的子問題。對於k類問題,最簡潔的分解方法是利用
個二分類器[Mayoraz,Moreira(1996)]。下表給出了一個四分類問題的緻密矩陣的例子。
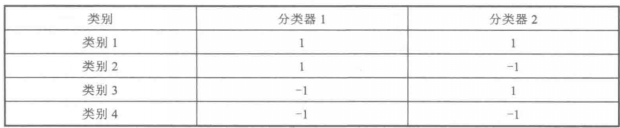 一個四分類問題的緻密編碼矩陣
一個四分類問題的緻密編碼矩陣對於一個七類問題,鑒於f=-f,不同的二分類器的總數為0.5(3k+1)-2k。換句話說,正的和負的類標的轉置產生同樣的分類器[Mayoraz,Moreira(1996)]。其中,2k-1—1同時包含所有的類,即它們僅有類別標識+1和-1,而沒有0的選項。包含這樣的分類器的一個四分類問題的編碼矩陣的例子如下表所列。
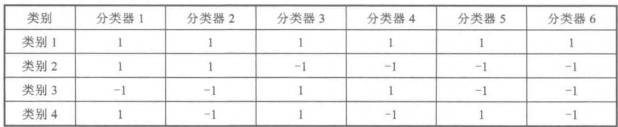 一個四分類問題的編碼矩陣
一個四分類問題的編碼矩陣下面ECOC矩陣的策略,即具有糾錯能力的編碼矩陣,以及其他獲得編碼矩陣的策略。
除非特別說明,以下的內容均採用二分類編碼矩陣,即矩陣的每項僅從+1和-1中取值。
Dietterich和Bariki[Dietterich,Bariki(1995)]認為在設計ECOC矩陣時,為確保糾錯能力必須具備兩個條件:行可分;列可分。
其中可分性通過海明距離來度量,等於不同位串間的差異。
還要避免常數列(僅包括正項或負項),因為它們不能表示一個二元決策問題。
令d
m表示
中任一成對行之間的最小海明距離。最終的ECOC多類分類器能夠對二分類器的輸出的糾錯能力至少為
。因此,按照海明距離,每個包含
個錯誤的不正確的分類都存在一個整體與正確類別碼書之間的偏差,而最鄰近的碼書就是正確的類另lJ[Dietterich,Bakiri(1995)]。這就是為什麼要求行可分的原因。按照這一原理,1AA編碼就不具有任何糾錯能力,因為d
m=2。列可分在設計電信領域的糾錯編碼時也是必需的[Alba,Chicano(2004)]。
除了以上的要求,二分類器的誤差必須是不相關的,以便在解決多類問題時可獲得好的糾錯編碼。為了滿足這一條件,必須是列可分的,即
中任一成對列之間的海明距離必須足夠大。如果在學習算法中,正的和負的類標的轉置產生同樣的分類器(f=-f),則每列與其他列之間的海明距離必須是最大的。
基於以上的討論,Dietterich和Bariki fDieRefich,Bariki(1995)]提出了4種技術用於設計具有好的糾錯能力的編碼矩陣。選擇哪種技術取決於多類問題的類別數。但是對於哪種方法適用於多少類別並沒有嚴格的規定。
對於k≤7,建議採用窮舉編碼。第一行(第一類的碼書)僅取值+1。所有其他行輪流取2k-i個正值和負值,i為行的數目。下表展示了四類問題的窮舉編碼矩陣的示例。
 一個四分類問題的緻密編碼矩陣
一個四分類問題的緻密編碼矩陣如果8≤k≤11,建議採用一個從窮舉編碼中選擇列的方法。
如果k>11,有兩個選項:一個是基於爬山算法的方法:另一個是BCH生成(Bose-Chaudhuri and Hocquenghem)編碼方法[Boser,Ray-Chaudhuri(1 960)]。
BCH套用多項式函式來設計接近最優的糾錯編碼。BCH編碼的一個問題是不能確保好的列可分。另外,如果類別數不是2的冪次方,則為了保持好的行和列的可分性,必須通過移動行(也可能是列)來縮短編碼。
Pimenta和Gama[Pimenta,Gama(2005)]提出了一個算法用於設計ECOC,獲得了比傳統分解方法更好的預測性能,他們採用決策樹(DTs)[Quinlan(1986)]和SVMs算法作為基分類器。他們採用一個函式,按照其糾錯能力來評估ECOC的性能。一個疊代破壞算法(PA)被用來構建ECOC,該算法通過對初始ECOC增加或者移除列來最大化性能函式。
一個好的ECOC是最大化碼書間的最小海明距離的編碼。因此,定義了一個線性函式
,其中
,
。此線性函式表示給定的k(類別數)和e(碼書長度)的最小海明距離。因為海明距離是整數值,所以支持函式a(k,e)被定義為y(k,e)的下界取整。基於此支持函式,可定義一個ECOC的性能函式q(k,e1(假設W,B,B+滿足W<B<B+)。
(1)當ECOC的最小海明距離低於支持函式a(k,e)的程度大於距離1時,q(k,e)=W。
(2)當ECOC的最小海明距離低於支持函式a(k,e)的程度小於距離1時,q(k,e)=B。
(3)當ECOC的最小海明距離等於或大於支持函式a(k,e)時,q(k,e)=B+。
Pimenta和Gama[Pimenta,Gama(2005)]對比了拒斥算法(RA)和破壞算法(PA)的性能。RA對一個評價函式進行最大化,當dm增加時該函式的值變大。由於在設計一個ECOC時不要求行可分,所以評價函式被用來懲罰具有相同或互補列的矩陣。另外,遺傳算法(GAs)被用來設計編碼矩陣,用於最大化評價函式。RA用於GA的變異步驟中。實驗對比研究表明,PA在發現有效的ECOCs時的性能更好,這裡的性能度量標準是看是否能避免相同的、互補的以及常數的列:而RA的性能比較差。在可產生有效的ECOCs的方法中,PA總體上都完成得比較好,可獲得按照Pimenta和Gama所提出的評價函式來度量的高質量的ECOCs。Pimenta和Gama還提出了一個方法用於確定ECOC中的列的數目(分解中所用的分類器的個數)[Pimenta,Gama(2005)]。該方法通過考查一個評價函式來實現,此評價函式是基於不同大小的ECOC可糾錯的數目來構建的。
一些研究隨機設計的ECOC即可獲得好的多類預測’Ni胄E[Berger(1999);Windeatt;Ghaderi(2003);Tapia,et a1.(2003)]。Allwein等人[Allwein,et a1.(2000)]比較了兩種隨機設計的編碼矩陣:緻密的和疏鬆的。在緻密編碼矩陣的實驗中,產生10000個隨機編碼矩陣,每個矩陣有[10xlog2(k)]列,並且矩陣的每項以同等的機率取值為-1或+1。按照Dietterich和Bariki [Dietterich,Bariki(1995)]的建議,具有更高的dm並且沒有相同或互補列的矩陣被選中。在疏鬆編碼矩陣的實驗中,採用三元字元編碼,矩陣的列數為[15log2(k)],矩陣中每項取值為0的機率為0.5,取值為+1或-1的機率為0.25。同樣產生10000個隨機編碼矩陣,並選擇具有最高的dm值的矩陣。
Berger [Berger(1999)]給出了關於隨機矩陣之所以取得較好性能的統計意義的綜合的評論。該評論認為,從理論上來說隨機矩陣具有較好的行和列的可分性,尤其是當矩陣的列數增加時。然而,他也在評論中假定個體分類器的誤差是不相關的,這一假定在實際套用中並不現實。
Windeatt和Ghaderi [Windeatt,Ghaderi(2002)]也注意到了等距編碼矩陣的價值。在等距編碼中,各行之間的海明距離基本上是個常數。他們的實驗表明,如果
是一個等距編碼矩陣,則不同行的+1的個數的相等的,並且任一成對行之間的共同的+1的個數也是相等的。他們利用這一思想來從BCH編碼中選擇一個行的子集,進而產生等距編碼。他們從實驗上驗證了當採用多層感知器(MLP)和神經網路(NNs) [Haykin(1999)]作為基分類器,等距編碼在採用較短的編碼(更少的列)時,其性能要優於1AA和隨機編碼。隨著編碼的長度的增加,等距編碼的優勢就不再明顯,此時更傾向於採用隨機編碼。
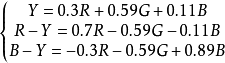
 電阻矩陣電路
電阻矩陣電路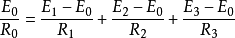




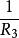


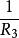


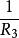


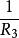


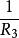

 一個四分類問題的緻密編碼矩陣
一個四分類問題的緻密編碼矩陣 一個四分類問題的編碼矩陣
一個四分類問題的編碼矩陣



 一個四分類問題的緻密編碼矩陣
一個四分類問題的緻密編碼矩陣